Noble C. Harasha
Deadlock and Noise in Self-Organized Aggregation Without Computation
Aug 20, 2021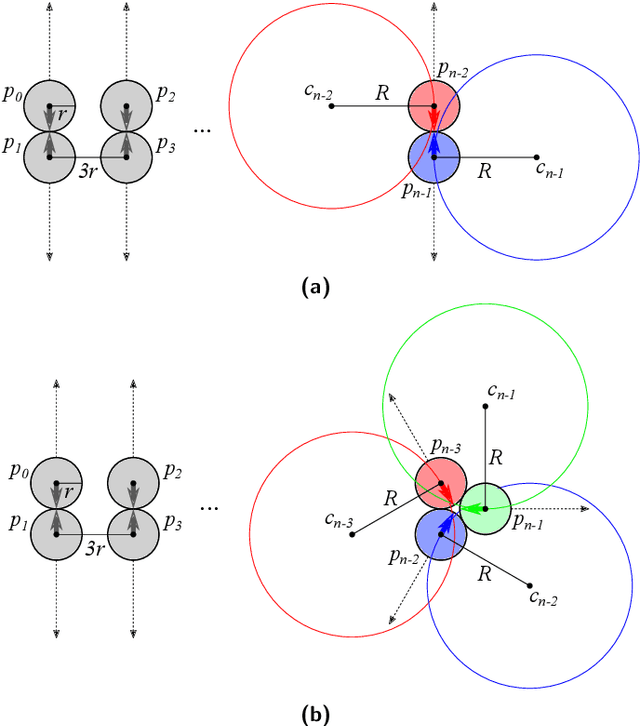
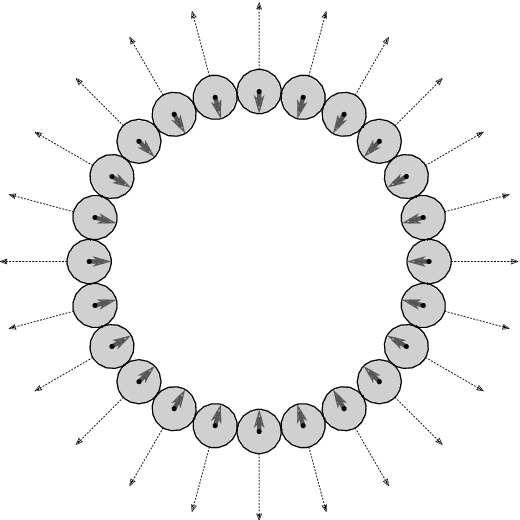
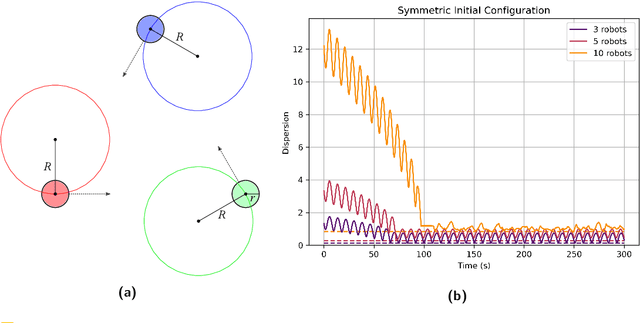
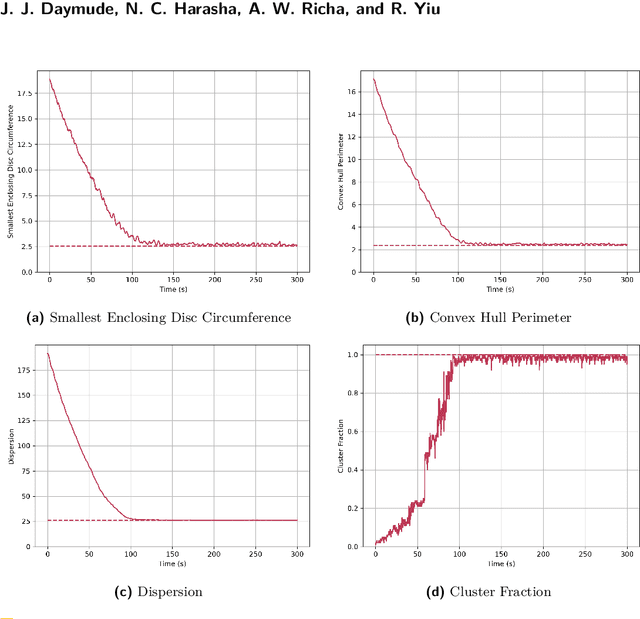
Abstract:Aggregation is a fundamental behavior for swarm robotics that requires a system to gather together in a compact, connected cluster. In 2014, Gauci et al. proposed a surprising algorithm that reliably achieves swarm aggregation using only a binary line-of-sight sensor and no arithmetic computation or persistent memory. It has been rigorously proven that this algorithm will aggregate one robot to another, but it remained open whether it would always aggregate a system of $n > 2$ robots as was observed in experiments and simulations. We prove that there exist deadlocked configurations from which this algorithm cannot achieve aggregation for $n > 3$ robots when the robots' motion is uniform and deterministic. On the positive side, we show that the algorithm (i) is robust to small amounts of error, enabling deadlock avoidance, and (ii) provably achieves a linear runtime speedup for the $n = 2$ case when using a cone-of-sight sensor. Finally, we introduce a noisy, discrete adaptation of this algorithm that is more amenable to rigorous analysis of noise and whose simulation results align qualitatively with the original, continuous algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge