Fault Localisation in Infinite-Dimensional Linear Electrical Networks

We present a novel fault localisation methodology for linear time-invariant electrical networks with infinite-dimensional edge dynamics and uncertain fault dynamics. The theory accommodates instability and also bounded propagation delays in the network. The goal is to estimate the location of a fault along a given network edge, using sensors positioned arbitrarily throughout the network. Passive faults of unknown impedance are considered, along with stable faults of known impedance. To illustrate the approach, we tackle a significant use-case: a multi-conductor transmission line, with dynamics modelled by the Telegrapher's equation, subject to a line-to-ground fault. Frequency-domain insights are used to reformulate the general fault localisation problem into a non-convex scalar optimisation problem, of which the true fault location is guaranteed to be a global minimiser. Numerical experiments are run to quantify localisation performance over a range of fault resistances.

ON-Traffic: An Operator Learning Framework for Online Traffic Flow Estimation and Uncertainty Quantification from Lagrangian Sensors

Accurate traffic flow estimation and prediction are critical for the efficient management of transportation systems, particularly under increasing urbanization. Traditional methods relying on static sensors often suffer from limited spatial coverage, while probe vehicles provide richer, albeit sparse and irregular data. This work introduces ON-Traffic, a novel deep operator Network and a receding horizon learning-based framework tailored for online estimation of spatio-temporal traffic state along with quantified uncertainty by using measurements from moving probe vehicles and downstream boundary inputs. Our framework is evaluated in both numerical and simulation datasets, showcasing its ability to handle irregular, sparse input data, adapt to time-shifted scenarios, and provide well-calibrated uncertainty estimates. The results demonstrate that the model captures complex traffic phenomena, including shockwaves and congestion propagation, while maintaining robustness to noise and sensor dropout. These advancements present a significant step toward online, adaptive traffic management systems.

Electrical Fault Localisation Over a Distributed Parameter Transmission Line

Motivated by the need to localise faults along electrical power lines, this paper adopts a frequency-domain approach to parameter estimation for an infinite-dimensional linear dynamical system with one spatial variable. Since the time of the fault is unknown, and voltages and currents are measured at only one end of the line, distance information must be extracted from the post-fault transients. To properly account for high-frequency transient behaviour, the line dynamics is modelled directly by the Telegrapher's equation, rather than the more commonly used lumped-parameter approximations. First, the governing equations are non-dimensionalised to avoid ill-conditioning. A closed-form expression for the transfer function is then derived. Finally, nonlinear least-squares optimisation is employed to search for the fault location. Requirements on fault bandwidth, sensor bandwidth and simulation time-step are also presented. The result is a novel end-to-end algorithm for data generation and fault localisation, the effectiveness of which is demonstrated via simulation.

Learning Flow Functions from Data with Applications to Nonlinear Oscillators

We describe a recurrent neural network (RNN) based architecture to learn the flow function of a causal, time-invariant and continuous-time control system from trajectory data. By restricting the class of control inputs to piecewise constant functions, we show that learning the flow function is equivalent to learning the input-to-state map of a discrete-time dynamical system. This motivates the use of an RNN together with encoder and decoder networks which map the state of the system to the hidden state of the RNN and back. We show that the proposed architecture is able to approximate the flow function by exploiting the system's causality and time-invariance. The output of the learned flow function model can be queried at any time instant. We experimentally validate the proposed method using models of the Van der Pol and FitzHugh Nagumo oscillators. In both cases, the results demonstrate that the architecture is able to closely reproduce the trajectories of these two systems. For the Van der Pol oscillator, we further show that the trained model generalises to the system's response with a prolonged prediction time horizon as well as control inputs outside the training distribution. For the FitzHugh-Nagumo oscillator, we show that the model accurately captures the input-dependent phenomena of excitability.

Learning-based Design of Luenberger Observers for Autonomous Nonlinear Systems

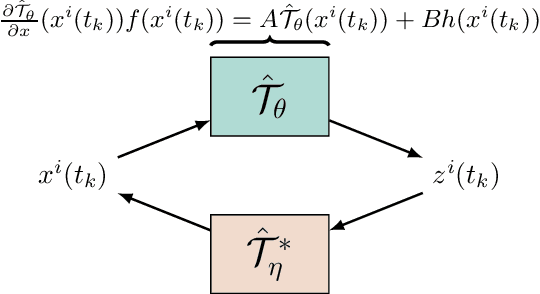
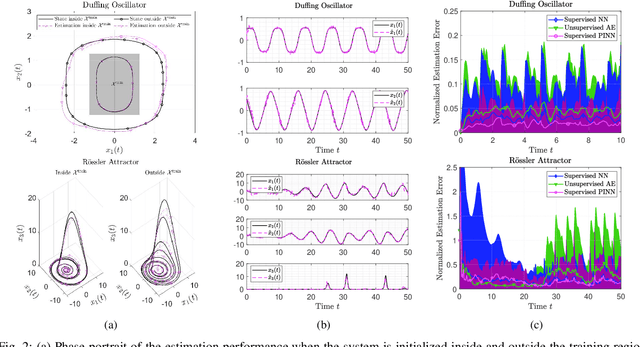
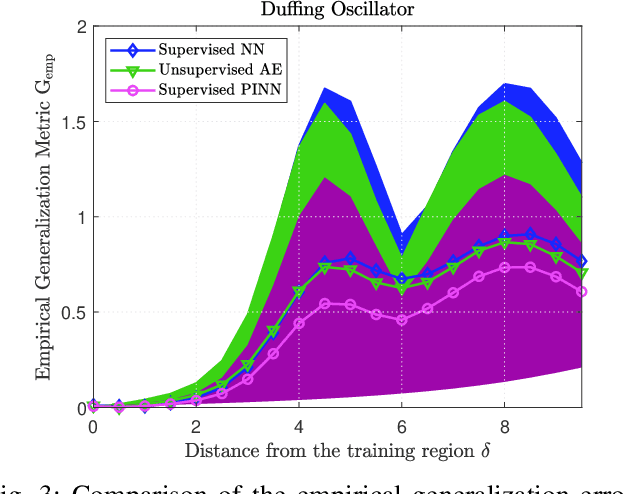
The design of Luenberger observers for nonlinear systems involves state transformation to another coordinate system where the dynamics are asymptotically stable and linear up to output injection. The observer then provides a state estimate in the original coordinates by inverting the transformation map. For general nonlinear systems, however, the main challenge is to find such a transformation and to ensure that it is injective. This paper addresses this challenge by proposing a learning method that employs supervised physics-informed neural networks to approximate both the transformation and its inverse. It is shown that the proposed method exhibits better generalization capabilities than other contemporary methods. Moreover, the observer is shown to be robust under the neural network's approximation error and the system uncertainties.