Learning-based Design of Luenberger Observers for Autonomous Nonlinear Systems

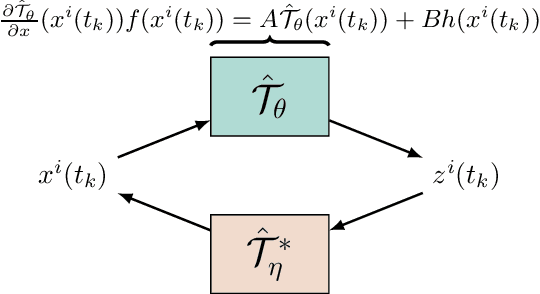
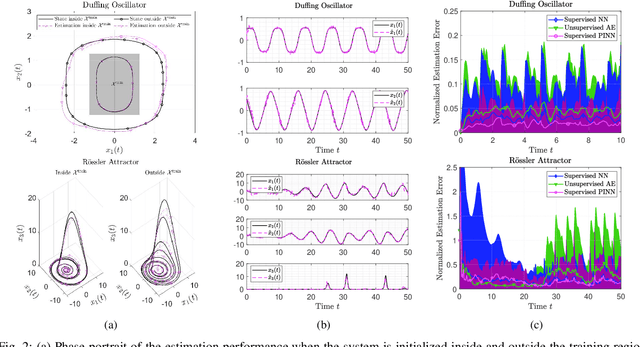
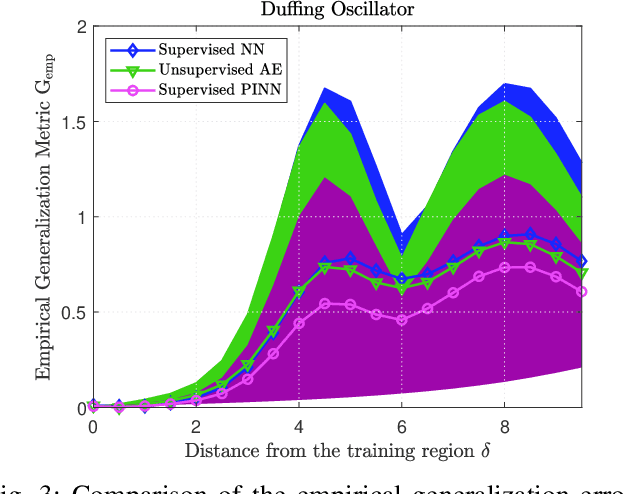
The design of Luenberger observers for nonlinear systems involves state transformation to another coordinate system where the dynamics are asymptotically stable and linear up to output injection. The observer then provides a state estimate in the original coordinates by inverting the transformation map. For general nonlinear systems, however, the main challenge is to find such a transformation and to ensure that it is injective. This paper addresses this challenge by proposing a learning method that employs supervised physics-informed neural networks to approximate both the transformation and its inverse. It is shown that the proposed method exhibits better generalization capabilities than other contemporary methods. Moreover, the observer is shown to be robust under the neural network's approximation error and the system uncertainties.