Sensor Fault Detection and Isolation in Autonomous Nonlinear Systems Using Neural Network-Based Observers

This paper presents a new observer-based approach to detect and isolate faulty sensors in industrial systems. Two types of sensor faults are considered: complete failure and sensor deterioration. The proposed method is applicable to general autonomous nonlinear systems without making any assumptions about its triangular and/or normal form, which is usually considered in the observer design literature. The key aspect of our approach is a learning-based design of the Luenberger observer, which involves using a neural network to approximate the injective map that transforms the nonlinear system into a stable linear system with output injection. This learning-based Luenberger observer accurately estimates the system's state, allowing for the detection of sensor faults through residual generation. The residual is computed as the norm of the difference between the system's measured output and the observer's predicted output vectors. Fault isolation is achieved by comparing each sensor's measurement with its corresponding predicted value. We demonstrate the effectiveness of our approach in capturing and isolating sensor faults while remaining robust in the presence of measurement noise and system uncertainty. We validate our method through numerical simulations of sensor faults in a network of Kuramoto oscillators.

Learning-based Design of Luenberger Observers for Autonomous Nonlinear Systems

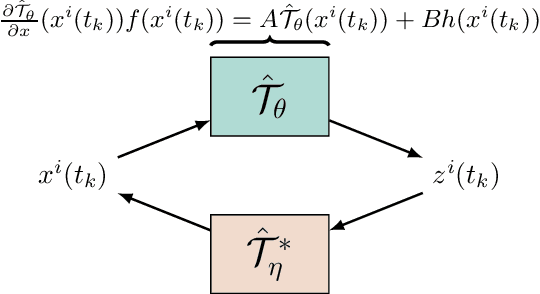
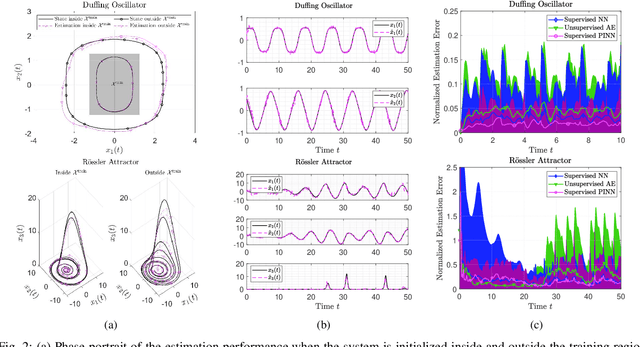
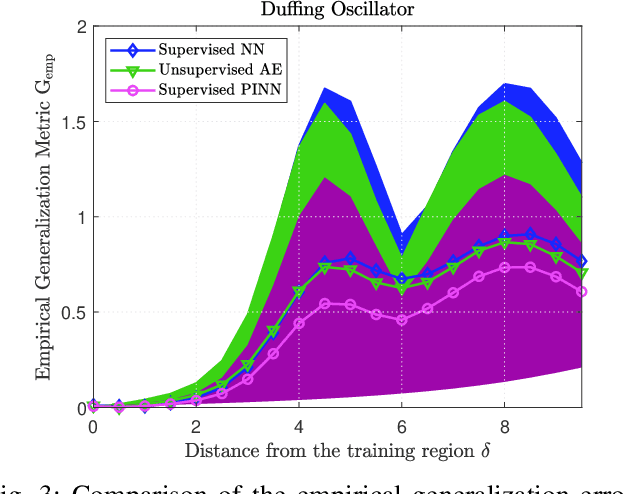
The design of Luenberger observers for nonlinear systems involves state transformation to another coordinate system where the dynamics are asymptotically stable and linear up to output injection. The observer then provides a state estimate in the original coordinates by inverting the transformation map. For general nonlinear systems, however, the main challenge is to find such a transformation and to ensure that it is injective. This paper addresses this challenge by proposing a learning method that employs supervised physics-informed neural networks to approximate both the transformation and its inverse. It is shown that the proposed method exhibits better generalization capabilities than other contemporary methods. Moreover, the observer is shown to be robust under the neural network's approximation error and the system uncertainties.

Data-driven Set-based Estimation of Polynomial Systems with Application to SIR Epidemics

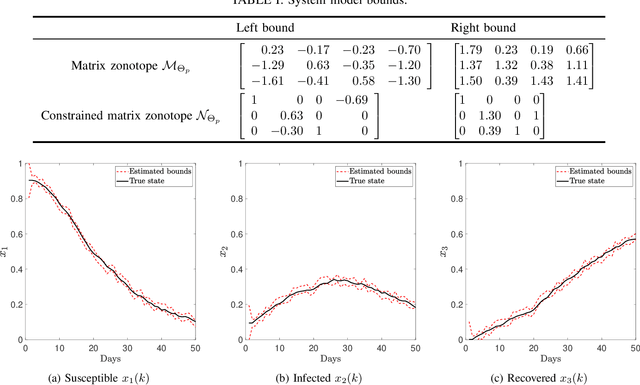
This paper proposes a data-driven set-based estimation algorithm for a class of nonlinear systems with polynomial nonlinearities. Using the system's input-output data, the proposed method computes in real-time a set that guarantees the inclusion of the system's state. Although the system is assumed to be polynomial type, the exact polynomial functions and their coefficients need not be known. To this end, the estimator relies on offline and online phases. The offline phase utilizes past input-output data to estimate a set of possible coefficients of the polynomial system. Then, using this estimated set of coefficients and the side information about the system, the online phase provides a set estimate of the state. Finally, the proposed methodology is evaluated through its application on SIR (Susceptible, Infected, Recovered) epidemic model.