Fault Localisation in Infinite-Dimensional Linear Electrical Networks

We present a novel fault localisation methodology for linear time-invariant electrical networks with infinite-dimensional edge dynamics and uncertain fault dynamics. The theory accommodates instability and also bounded propagation delays in the network. The goal is to estimate the location of a fault along a given network edge, using sensors positioned arbitrarily throughout the network. Passive faults of unknown impedance are considered, along with stable faults of known impedance. To illustrate the approach, we tackle a significant use-case: a multi-conductor transmission line, with dynamics modelled by the Telegrapher's equation, subject to a line-to-ground fault. Frequency-domain insights are used to reformulate the general fault localisation problem into a non-convex scalar optimisation problem, of which the true fault location is guaranteed to be a global minimiser. Numerical experiments are run to quantify localisation performance over a range of fault resistances.

Electrical Fault Localisation Over a Distributed Parameter Transmission Line

Motivated by the need to localise faults along electrical power lines, this paper adopts a frequency-domain approach to parameter estimation for an infinite-dimensional linear dynamical system with one spatial variable. Since the time of the fault is unknown, and voltages and currents are measured at only one end of the line, distance information must be extracted from the post-fault transients. To properly account for high-frequency transient behaviour, the line dynamics is modelled directly by the Telegrapher's equation, rather than the more commonly used lumped-parameter approximations. First, the governing equations are non-dimensionalised to avoid ill-conditioning. A closed-form expression for the transfer function is then derived. Finally, nonlinear least-squares optimisation is employed to search for the fault location. Requirements on fault bandwidth, sensor bandwidth and simulation time-step are also presented. The result is a novel end-to-end algorithm for data generation and fault localisation, the effectiveness of which is demonstrated via simulation.

Lazy Probabilistic Roadmaps Revisited

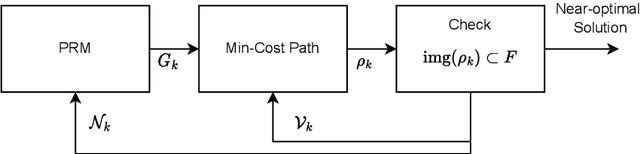
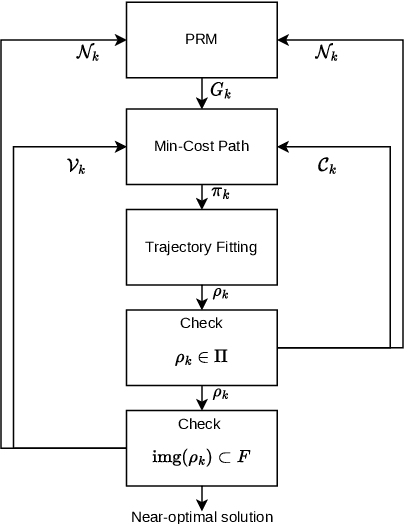
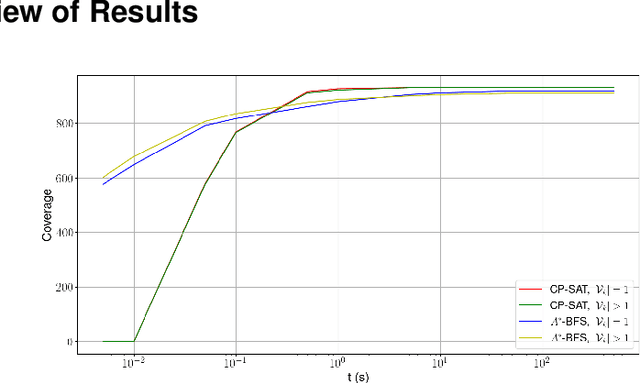
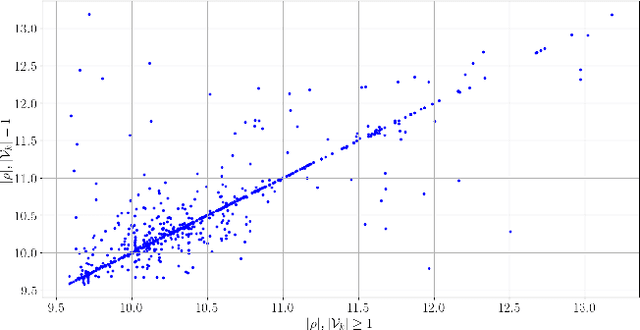
This paper describes a revision of the classic Lazy Probabilistic Roadmaps algorithm (Lazy PRM), that results from pairing PRM and a novel Branch-and-Cut (BC) algorithm. Cuts are dynamically generated constraints that are imposed on minimum cost paths over the geometric graphs selected by PRM. Cuts eliminate paths that cannot be mapped into smooth plans that satisfy suitably defined kinematic constraints. We generate candidate smooth plans by fitting splines to vertices in minimum-cost path. Plans are validated with a recently proposed algorithm that maps them into finite traces, without need to choose a fixed discretization step. Trace elements exactly describe when plans cross constraint boundaries modulo arithmetic precision. We evaluate several planners using our methods over the recently proposed BARN benchmark, and we report evidence of the scalability of our approach.