On the Uniqueness of Solution for the Bellman Equation of LTL Objectives

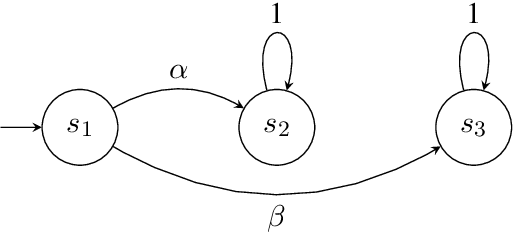
Surrogate rewards for linear temporal logic (LTL) objectives are commonly utilized in planning problems for LTL objectives. In a widely-adopted surrogate reward approach, two discount factors are used to ensure that the expected return approximates the satisfaction probability of the LTL objective. The expected return then can be estimated by methods using the Bellman updates such as reinforcement learning. However, the uniqueness of the solution to the Bellman equation with two discount factors has not been explicitly discussed. We demonstrate with an example that when one of the discount factors is set to one, as allowed in many previous works, the Bellman equation may have multiple solutions, leading to inaccurate evaluation of the expected return. We then propose a condition for the Bellman equation to have the expected return as the unique solution, requiring the solutions for states inside a rejecting bottom strongly connected component (BSCC) to be 0. We prove this condition is sufficient by showing that the solutions for the states with discounting can be separated from those for the states without discounting under this condition

Reinforcement Learning with Temporal Logic Constraints for Partially-Observable Markov Decision Processes

This paper proposes a reinforcement learning method for controller synthesis of autonomous systems in unknown and partially-observable environments with subjective time-dependent safety constraints. Mathematically, we model the system dynamics by a partially-observable Markov decision process (POMDP) with unknown transition/observation probabilities. The time-dependent safety constraint is captured by iLTL, a variation of linear temporal logic for state distributions. Our Reinforcement learning method first constructs the belief MDP of the POMDP, capturing the time evolution of estimated state distributions. Then, by building the product belief MDP of the belief MDP and the limiting deterministic B\uchi automaton (LDBA) of the temporal logic constraint, we transform the time-dependent safety constraint on the POMDP into a state-dependent constraint on the product belief MDP. Finally, we learn the optimal policy by value iteration under the state-dependent constraint.

Model-Free Learning of Safe yet Effective Controllers

In this paper, we study the problem of learning safe control policies that are also effective -- i.e., maximizing the probability of satisfying the linear temporal logic (LTL) specification of the task, and the discounted reward capturing the (classic) control performance. We consider unknown environments that can be modeled as Markov decision processes (MDPs). We propose a model-free reinforcement learning algorithm that learns a policy that first maximizes the probability of ensuring the safety, then the probability of satisfying the given LTL specification and lastly, the sum of discounted Quality of Control (QoC) rewards. Finally, we illustrate the applicability of our RL-based approach on a case study.

Learning Optimal Strategies for Temporal Tasks in Stochastic Games

Linear temporal logic (LTL) is widely used to formally specify complex tasks for autonomy. Unlike usual tasks defined by reward functions only, LTL tasks are noncumulative and require memory-dependent strategies. In this work, we introduce a method to learn optimal controller strategies that maximize the satisfaction probability of LTL specifications of the desired tasks in stochastic games, which are natural extensions of Markov Decision Processes (MDPs) to systems with adversarial inputs. Our approach constructs a product game using the deterministic automaton derived from the given LTL task and a reward machine based on the acceptance condition of the automaton; thus, allowing for the use of a model-free RL algorithm to learn an optimal controller strategy. Since the rewards and the transition probabilities of the reward machine do not depend on the number of sets defining the acceptance condition, our approach is scalable to a wide range of LTL tasks, as we demonstrate on several case studies.

Secure Planning Against Stealthy Attacks via Model-Free Reinforcement Learning

We consider the problem of security-aware planning in an unknown stochastic environment, in the presence of attacks on control signals (i.e., actuators) of the robot. We model the attacker as an agent who has the full knowledge of the controller as well as the employed intrusion-detection system and who wants to prevent the controller from performing tasks while staying stealthy. We formulate the problem as a stochastic game between the attacker and the controller and present an approach to express the objective of such an agent and the controller as a combined linear temporal logic (LTL) formula. We then show that the planning problem, described formally as the problem of satisfying an LTL formula in a stochastic game, can be solved via model-free reinforcement learning when the environment is completely unknown. Finally, we illustrate and evaluate our methods on two robotic planning case studies.

Model-Free Reinforcement Learning for Stochastic Games with Linear Temporal Logic Objectives

We study the problem of synthesizing control strategies for Linear Temporal Logic (LTL) objectives in unknown environments. We model this problem as a turn-based zero-sum stochastic game between the controller and the environment, where the transition probabilities and the model topology are fully unknown. The winning condition for the controller in this game is the satisfaction of the given LTL specification, which can be captured by the acceptance condition of a deterministic Rabin automaton (DRA) directly derived from the LTL specification. We introduce a model-free reinforcement learning (RL) methodology to find a strategy that maximizes the probability of satisfying a given LTL specification when the Rabin condition of the derived DRA has a single accepting pair. We then generalize this approach to LTL formulas for which the Rabin condition has a larger number of accepting pairs, providing a lower bound on the satisfaction probability. Finally, we illustrate applicability of our RL method on two motion planning case studies.

Control Synthesis from Linear Temporal Logic Specifications using Model-Free Reinforcement Learning

We present a reinforcement learning (RL) framework to synthesize a control policy from a given linear temporal logic (LTL) specification in an unknown stochastic environment that can be modeled as a Markov Decision Process (MDP). Specifically, we learn a policy that maximizes the probability of satisfying the LTL formula without learning the transition probabilities. We introduce a novel rewarding and path-dependent discounting mechanism based on the LTL formula such that (i) an optimal policy maximizing the total discounted reward effectively maximizes the probabilities of satisfying LTL objectives, and (ii) a model-free RL algorithm using these rewards and discount factors is guaranteed to converge to such policy. Finally, we illustrate the applicability of our RL-based synthesis approach on two motion planning case studies.