A Cluster-Cumulant Expansion at the Fixed Points of Belief Propagation

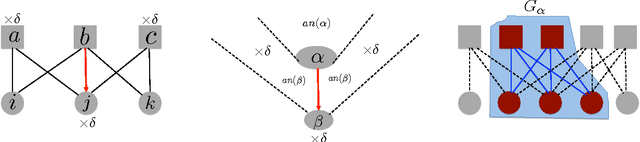
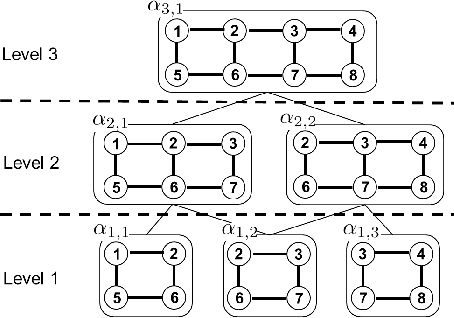
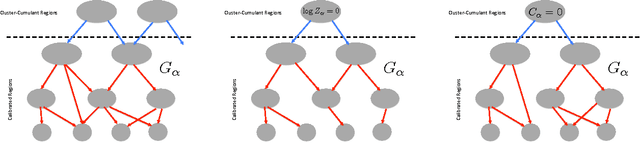
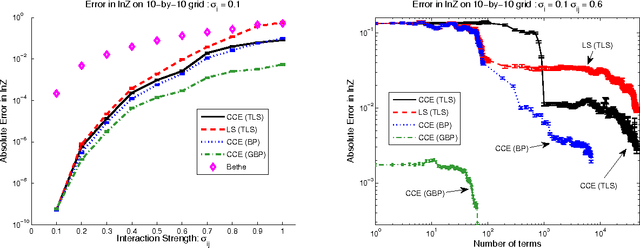
We introduce a new cluster-cumulant expansion (CCE) based on the fixed points of iterative belief propagation (IBP). This expansion is similar in spirit to the loop-series (LS) recently introduced in [1]. However, in contrast to the latter, the CCE enjoys the following important qualities: 1) it is defined for arbitrary state spaces 2) it is easily extended to fixed points of generalized belief propagation (GBP), 3) disconnected groups of variables will not contribute to the CCE and 4) the accuracy of the expansion empirically improves upon that of the LS. The CCE is based on the same M\"obius transform as the Kikuchi approximation, but unlike GBP does not require storing the beliefs of the GBP-clusters nor does it suffer from convergence issues during belief updating.

Belief Propagation for Structured Decision Making

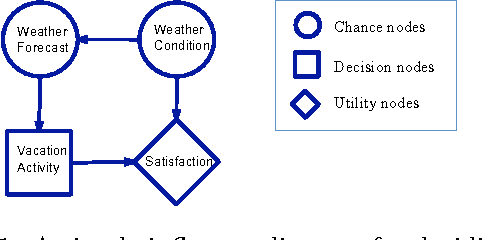
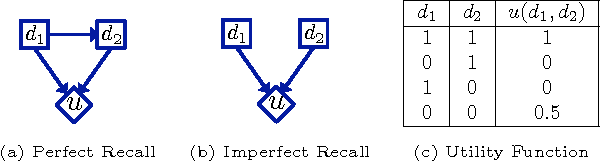
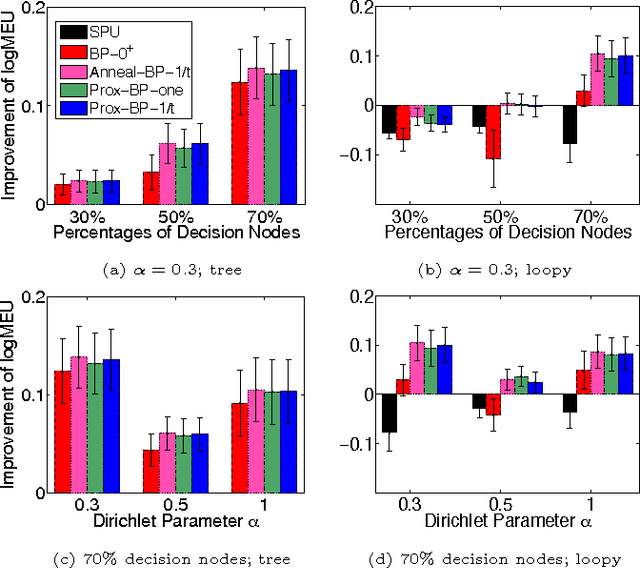
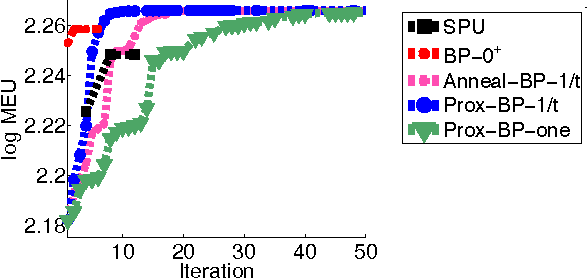
Variational inference algorithms such as belief propagation have had tremendous impact on our ability to learn and use graphical models, and give many insights for developing or understanding exact and approximate inference. However, variational approaches have not been widely adoped for decision making in graphical models, often formulated through influence diagrams and including both centralized and decentralized (or multi-agent) decisions. In this work, we present a general variational framework for solving structured cooperative decision-making problems, use it to propose several belief propagation-like algorithms, and analyze them both theoretically and empirically.

Join-graph based cost-shifting schemes

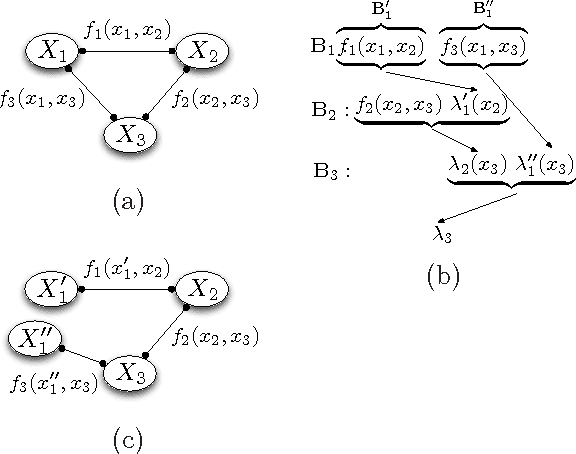
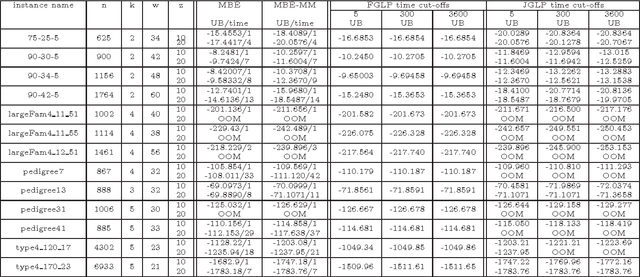
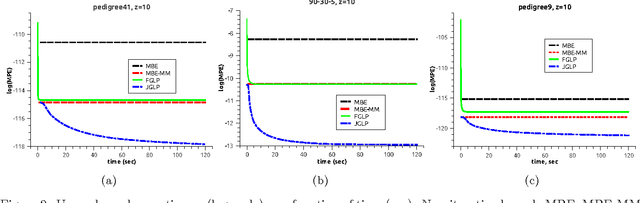
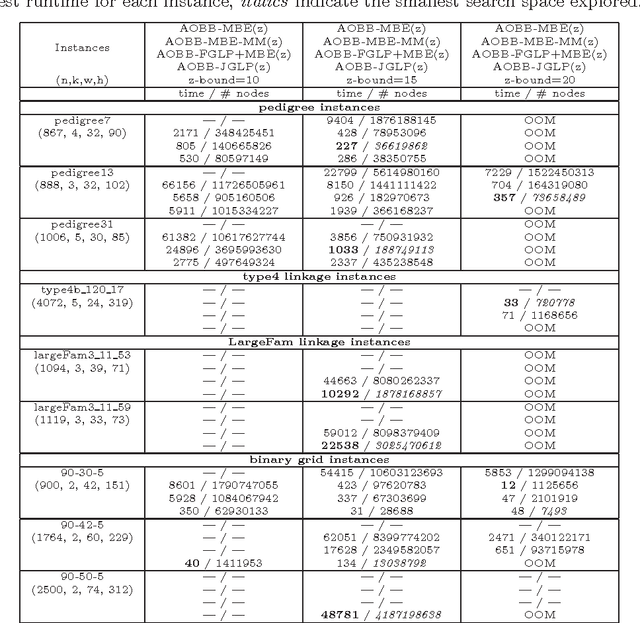
We develop several algorithms taking advantage of two common approaches for bounding MPE queries in graphical models: minibucket elimination and message-passing updates for linear programming relaxations. Both methods are quite similar, and offer useful perspectives for the other; our hybrid approaches attempt to balance the advantages of each. We demonstrate the power of our hybrid algorithms through extensive empirical evaluation. Most notably, a Branch and Bound search guided by the heuristic function calculated by one of our new algorithms has recently won first place in the PASCAL2 inference challenge.

Fast Planar Correlation Clustering for Image Segmentation

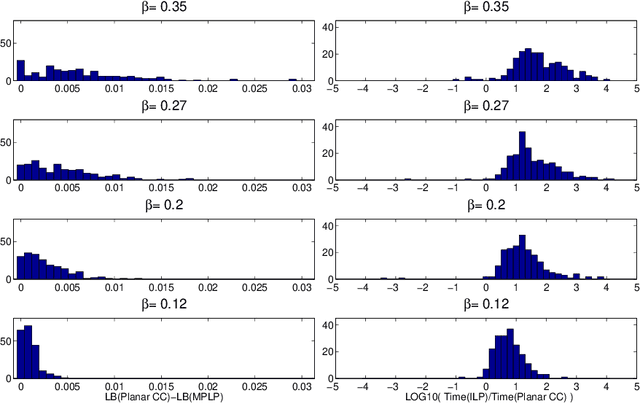
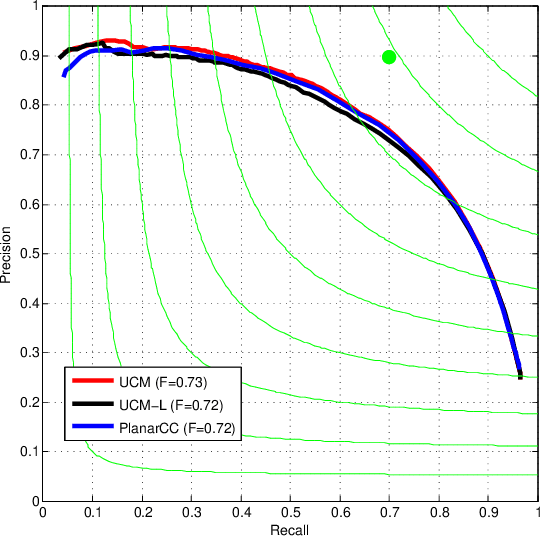
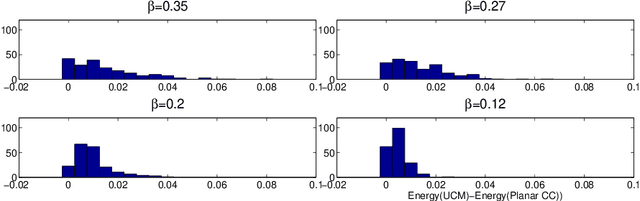
We describe a new optimization scheme for finding high-quality correlation clusterings in planar graphs that uses weighted perfect matching as a subroutine. Our method provides lower-bounds on the energy of the optimal correlation clustering that are typically fast to compute and tight in practice. We demonstrate our algorithm on the problem of image segmentation where this approach outperforms existing global optimization techniques in minimizing the objective and is competitive with the state of the art in producing high-quality segmentations.

Gibbs Sampling for Infinite Mixture Models in the Stick Breaking Representation

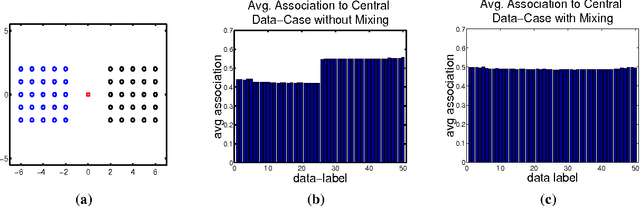
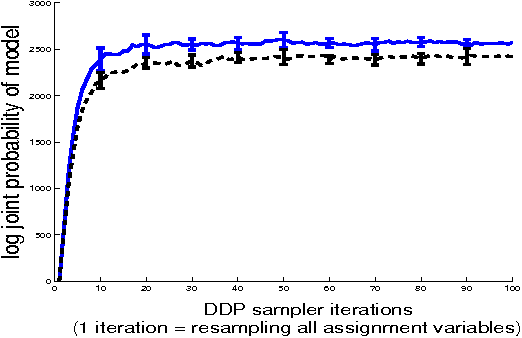
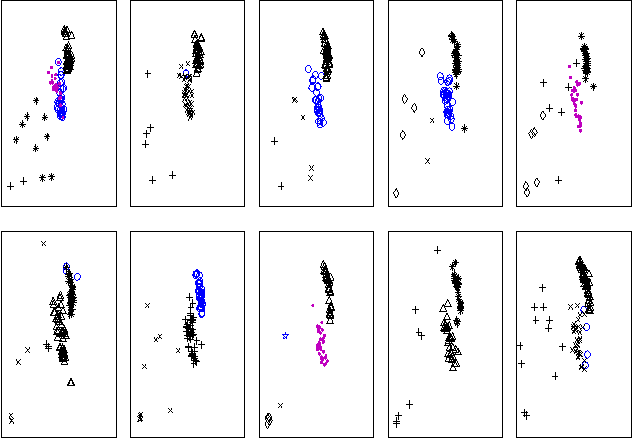
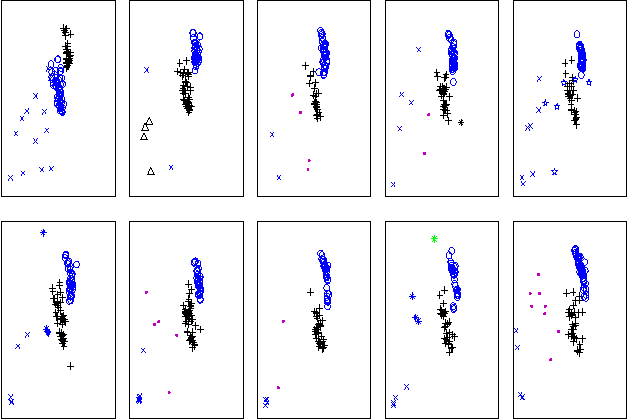
Nonparametric Bayesian approaches to clustering, information retrieval, language modeling and object recognition have recently shown great promise as a new paradigm for unsupervised data analysis. Most contributions have focused on the Dirichlet process mixture models or extensions thereof for which efficient Gibbs samplers exist. In this paper we explore Gibbs samplers for infinite complexity mixture models in the stick breaking representation. The advantage of this representation is improved modeling flexibility. For instance, one can design the prior distribution over cluster sizes or couple multiple infinite mixture models (e.g. over time) at the level of their parameters (i.e. the dependent Dirichlet process model). However, Gibbs samplers for infinite mixture models (as recently introduced in the statistics literature) seem to mix poorly over cluster labels. Among others issues, this can have the adverse effect that labels for the same cluster in coupled mixture models are mixed up. We introduce additional moves in these samplers to improve mixing over cluster labels and to bring clusters into correspondence. An application to modeling of storm trajectories is used to illustrate these ideas.

Accuracy Bounds for Belief Propagation

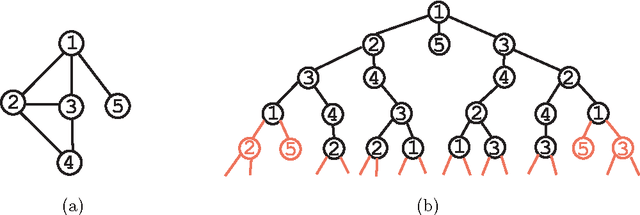
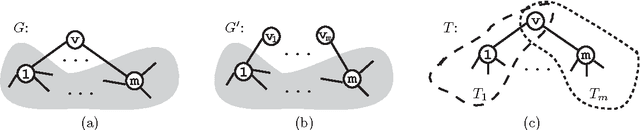
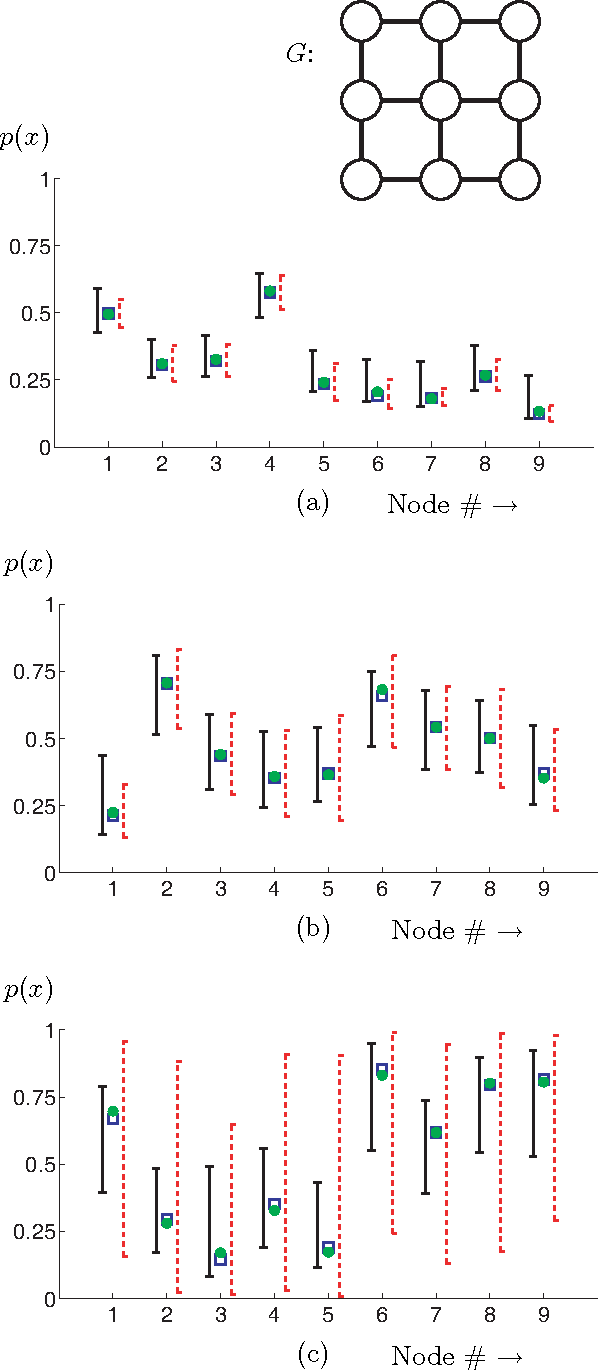
The belief propagation (BP) algorithm is widely applied to perform approximate inference on arbitrary graphical models, in part due to its excellent empirical properties and performance. However, little is known theoretically about when this algorithm will perform well. Using recent analysis of convergence and stability properties in BP and new results on approximations in binary systems, we derive a bound on the error in BP's estimates for pairwise Markov random fields over discrete valued random variables. Our bound is relatively simple to compute, and compares favorably with a previous method of bounding the accuracy of BP.

Adaptive Inference on General Graphical Models

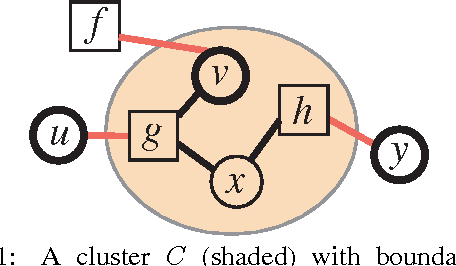
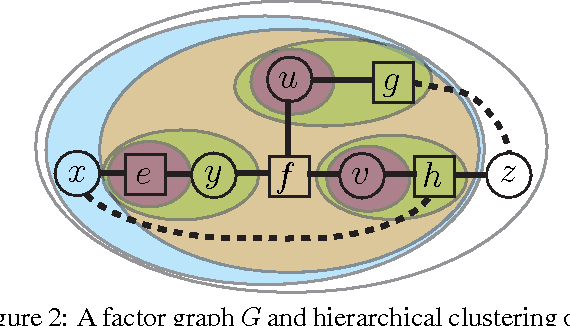
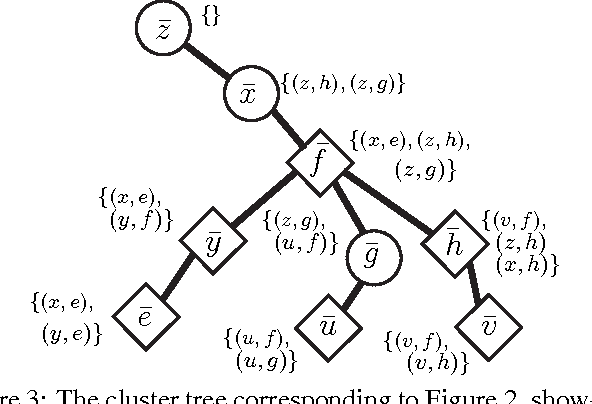
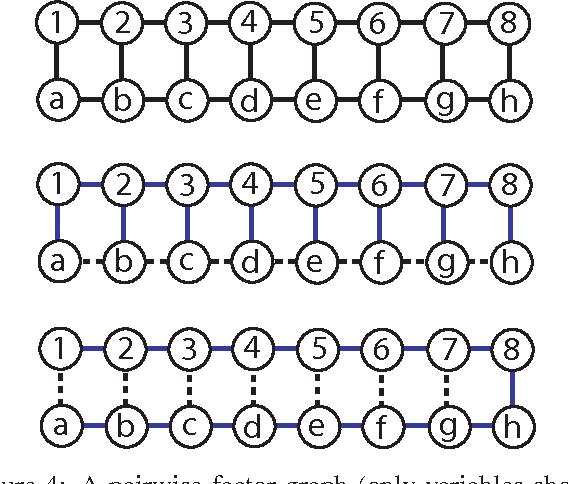
Many algorithms and applications involve repeatedly solving variations of the same inference problem; for example we may want to introduce new evidence to the model or perform updates to conditional dependencies. The goal of adaptive inference is to take advantage of what is preserved in the model and perform inference more rapidly than from scratch. In this paper, we describe techniques for adaptive inference on general graphs that support marginal computation and updates to the conditional probabilities and dependencies in logarithmic time. We give experimental results for an implementation of our algorithm, and demonstrate its potential performance benefit in the study of protein structure.

Negative Tree Reweighted Belief Propagation

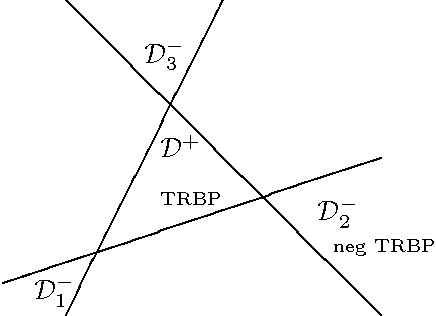
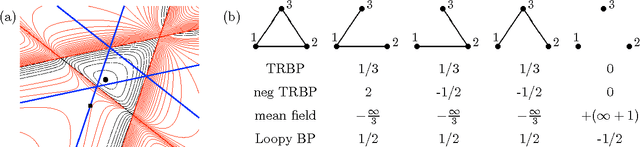
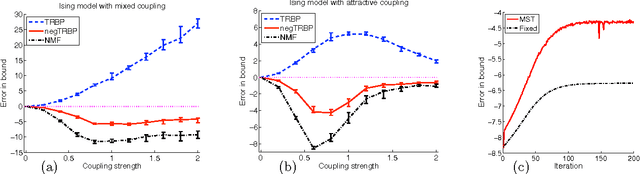
We introduce a new class of lower bounds on the log partition function of a Markov random field which makes use of a reversed Jensen's inequality. In particular, our method approximates the intractable distribution using a linear combination of spanning trees with negative weights. This technique is a lower-bound counterpart to the tree-reweighted belief propagation algorithm, which uses a convex combination of spanning trees with positive weights to provide corresponding upper bounds. We develop algorithms to optimize and tighten the lower bounds over the non-convex set of valid parameter values. Our algorithm generalizes mean field approaches (including naive and structured mean field approximations), which it includes as a limiting case.

Tightening MRF Relaxations with Planar Subproblems

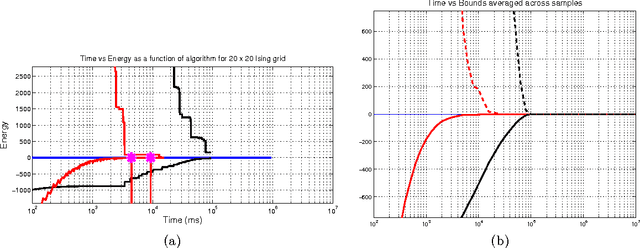
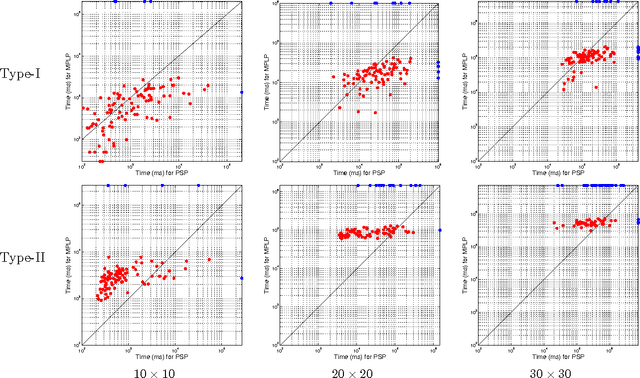
We describe a new technique for computing lower-bounds on the minimum energy configuration of a planar Markov Random Field (MRF). Our method successively adds large numbers of constraints and enforces consistency over binary projections of the original problem state space. These constraints are represented in terms of subproblems in a dual-decomposition framework that is optimized using subgradient techniques. The complete set of constraints we consider enforces cycle consistency over the original graph. In practice we find that the method converges quickly on most problems with the addition of a few subproblems and outperforms existing methods for some interesting classes of hard potentials.

Planar Cycle Covering Graphs

We describe a new variational lower-bound on the minimum energy configuration of a planar binary Markov Random Field (MRF). Our method is based on adding auxiliary nodes to every face of a planar embedding of the graph in order to capture the effect of unary potentials. A ground state of the resulting approximation can be computed efficiently by reduction to minimum-weight perfect matching. We show that optimization of variational parameters achieves the same lower-bound as dual-decomposition into the set of all cycles of the original graph. We demonstrate that our variational optimization converges quickly and provides high-quality solutions to hard combinatorial problems 10-100x faster than competing algorithms that optimize the same bound.