Andrew E. Gelfand
A Cluster-Cumulant Expansion at the Fixed Points of Belief Propagation
Oct 16, 2012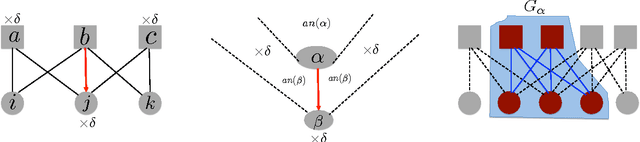
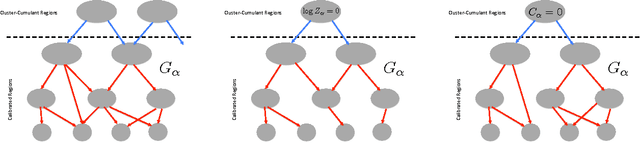
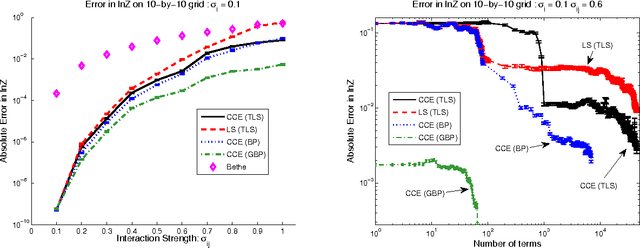
Abstract:We introduce a new cluster-cumulant expansion (CCE) based on the fixed points of iterative belief propagation (IBP). This expansion is similar in spirit to the loop-series (LS) recently introduced in [1]. However, in contrast to the latter, the CCE enjoys the following important qualities: 1) it is defined for arbitrary state spaces 2) it is easily extended to fixed points of generalized belief propagation (GBP), 3) disconnected groups of variables will not contribute to the CCE and 4) the accuracy of the expansion empirically improves upon that of the LS. The CCE is based on the same M\"obius transform as the Kikuchi approximation, but unlike GBP does not require storing the beliefs of the GBP-clusters nor does it suffer from convergence issues during belief updating.
Generalized Belief Propagation on Tree Robust Structured Region Graphs
Oct 16, 2012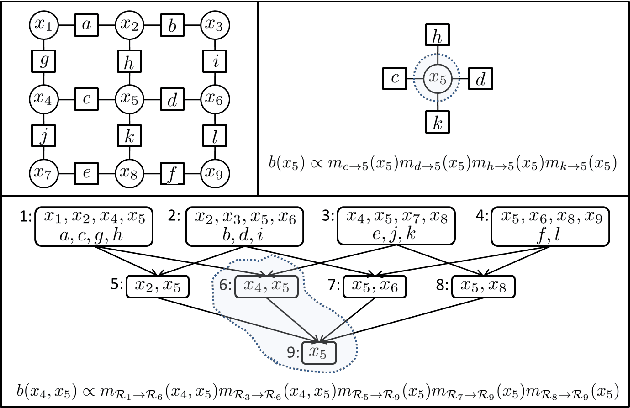
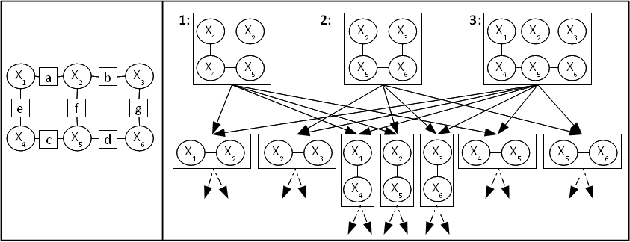
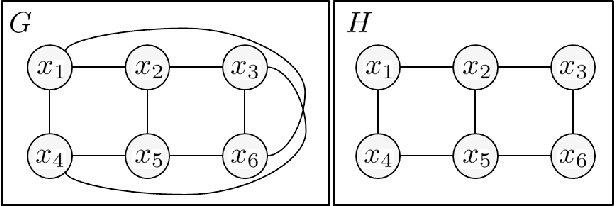
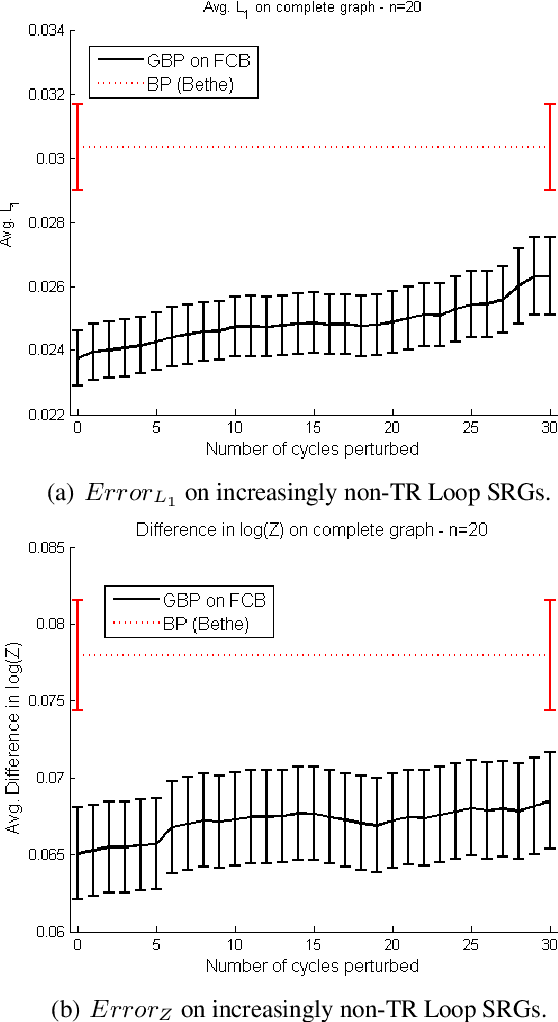
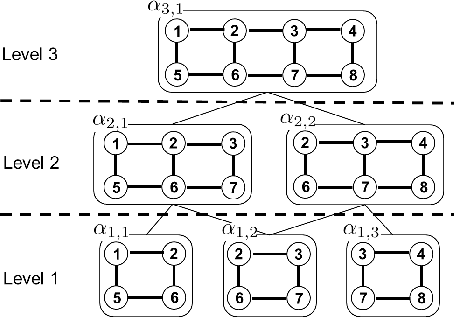
Abstract:This paper provides some new guidance in the construction of region graphs for Generalized Belief Propagation (GBP). We connect the problem of choosing the outer regions of a LoopStructured Region Graph (SRG) to that of finding a fundamental cycle basis of the corresponding Markov network. We also define a new class of tree-robust Loop-SRG for which GBP on any induced (spanning) tree of the Markov network, obtained by setting to zero the off-tree interactions, is exact. This class of SRG is then mapped to an equivalent class of tree-robust cycle bases on the Markov network. We show that a treerobust cycle basis can be identified by proving that for every subset of cycles, the graph obtained from the edges that participate in a single cycle only, is multiply connected. Using this we identify two classes of tree-robust cycle bases: planar cycle bases and "star" cycle bases. In experiments we show that tree-robustness can be successfully exploited as a design principle to improve the accuracy and convergence of GBP.
BEEM : Bucket Elimination with External Memory
Mar 15, 2012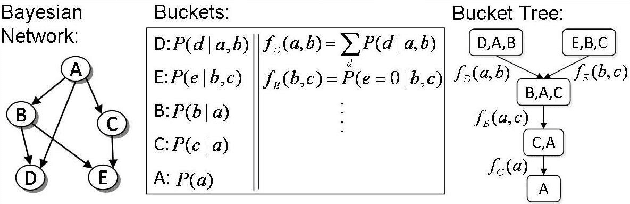
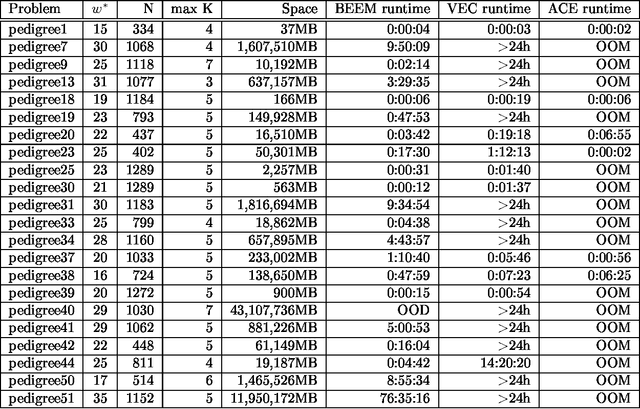

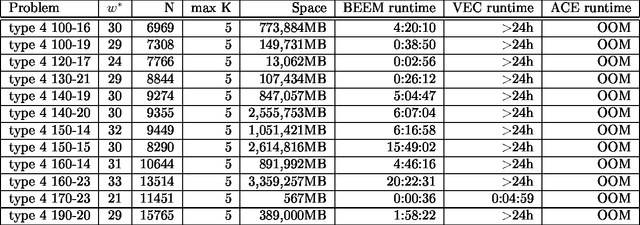
Abstract:A major limitation of exact inference algorithms for probabilistic graphical models is their extensive memory usage, which often puts real-world problems out of their reach. In this paper we show how we can extend inference algorithms, particularly Bucket Elimination, a special case of cluster (join) tree decomposition, to utilize disk memory. We provide the underlying ideas and show promising empirical results of exactly solving large problems not solvable before.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge