Join-Graph Propagation Algorithms

The paper investigates parameterized approximate message-passing schemes that are based on bounded inference and are inspired by Pearl's belief propagation algorithm (BP). We start with the bounded inference mini-clustering algorithm and then move to the iterative scheme called Iterative Join-Graph Propagation (IJGP), that combines both iteration and bounded inference. Algorithm IJGP belongs to the class of Generalized Belief Propagation algorithms, a framework that allowed connections with approximate algorithms from statistical physics and is shown empirically to surpass the performance of mini-clustering and belief propagation, as well as a number of other state-of-the-art algorithms on several classes of networks. We also provide insight into the accuracy of iterative BP and IJGP by relating these algorithms to well known classes of constraint propagation schemes.

Empirical Evaluation of Approximation Algorithms for Probabilistic Decoding

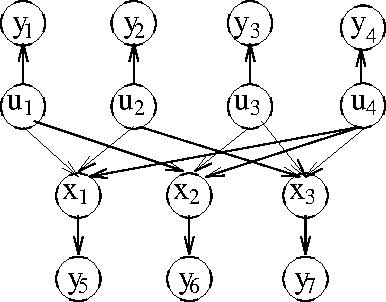
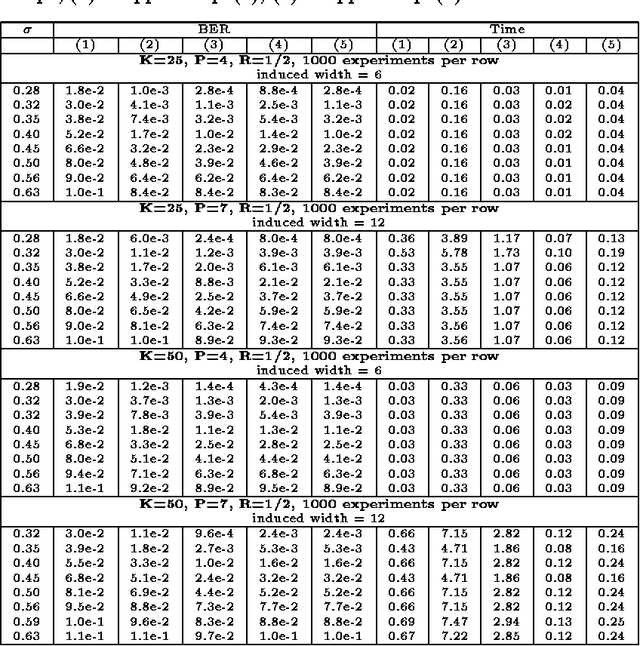
It was recently shown that the problem of decoding messages transmitted through a noisy channel can be formulated as a belief updating task over a probabilistic network [McEliece]. Moreover, it was observed that iterative application of the (linear time) Pearl's belief propagation algorithm designed for polytrees outperformed state of the art decoding algorithms, even though the corresponding networks may have many cycles. This paper demonstrates empirically that an approximation algorithm approx-mpe for solving the most probable explanation (MPE) problem, developed within the recently proposed mini-bucket elimination framework [Dechter96], outperforms iterative belief propagation on classes of coding networks that have bounded induced width. Our experiments suggest that approximate MPE decoders can be good competitors to the approximate belief updating decoders.

Mini-Bucket Heuristics for Improved Search

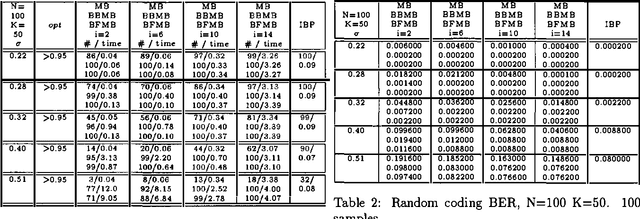
The paper is a second in a series of two papers evaluating the power of a new scheme that generates search heuristics mechanically. The heuristics are extracted from an approximation scheme called mini-bucket elimination that was recently introduced. The first paper introduced the idea and evaluated it within Branch-and-Bound search. In the current paper the idea is further extended and evaluated within Best-First search. The resulting algorithms are compared on coding and medical diagnosis problems, using varying strength of the mini-bucket heuristics. Our results demonstrate an effective search scheme that permits controlled tradeoff between preprocessing (for heuristic generation) and search. Best-first search is shown to outperform Branch-and-Bound, when supplied with good heuristics, and sufficient memory space.

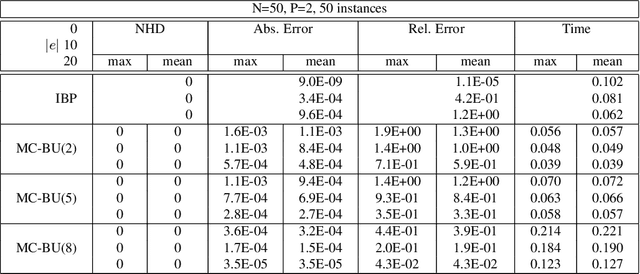
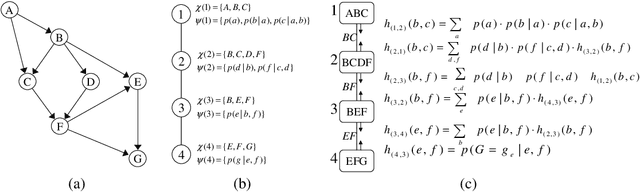
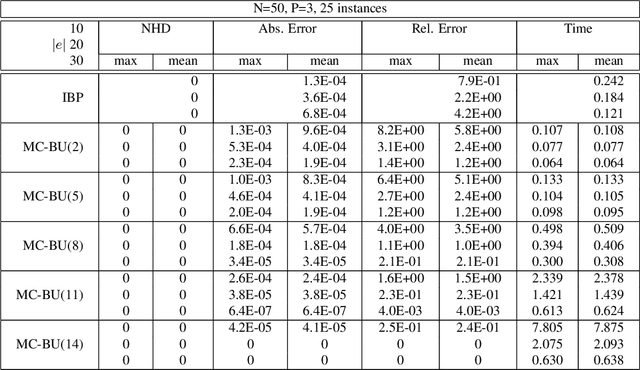
Iterative Join-Graph Propagation

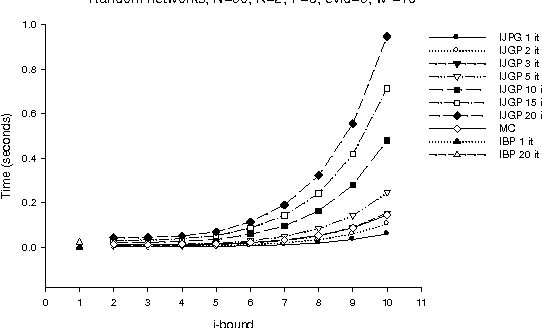
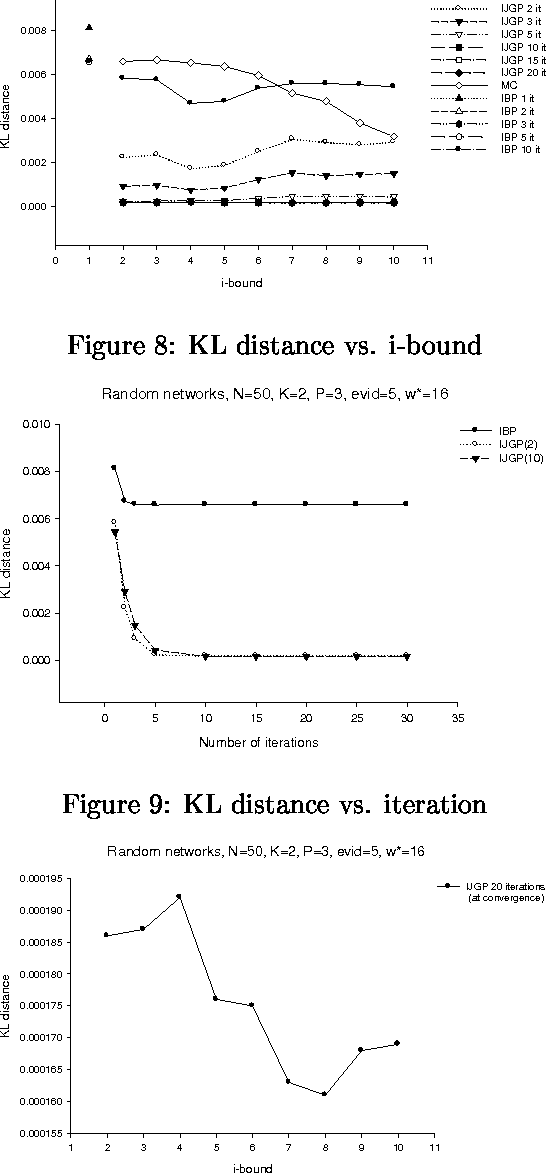
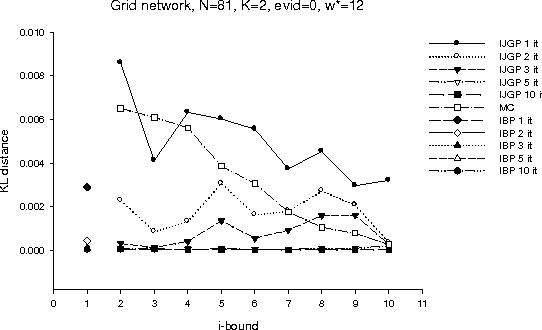
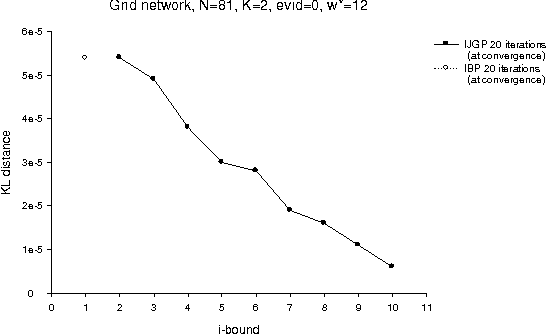
The paper presents an iterative version of join-tree clustering that applies the message passing of join-tree clustering algorithm to join-graphs rather than to join-trees, iteratively. It is inspired by the success of Pearl's belief propagation algorithm as an iterative approximation scheme on one hand, and by a recently introduced mini-clustering i. success as an anytime approximation method, on the other. The proposed Iterative Join-graph Propagation IJGP belongs to the class of generalized belief propagation methods, recently proposed using analogy with algorithms in statistical physics. Empirical evaluation of this approach on a number of problem classes demonstrates that even the most time-efficient variant is almost always superior to IBP and MC i, and is sometimes more accurate by as much as several orders of magnitude.

Systematic vs. Non-systematic Algorithms for Solving the MPE Task

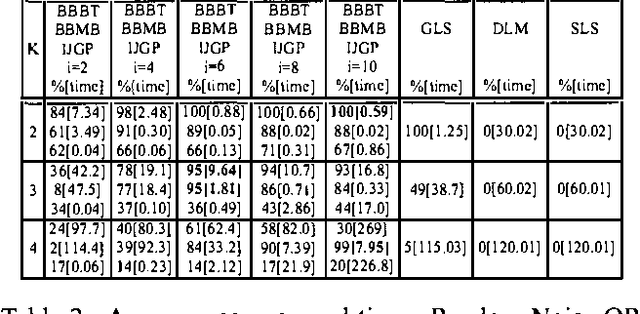
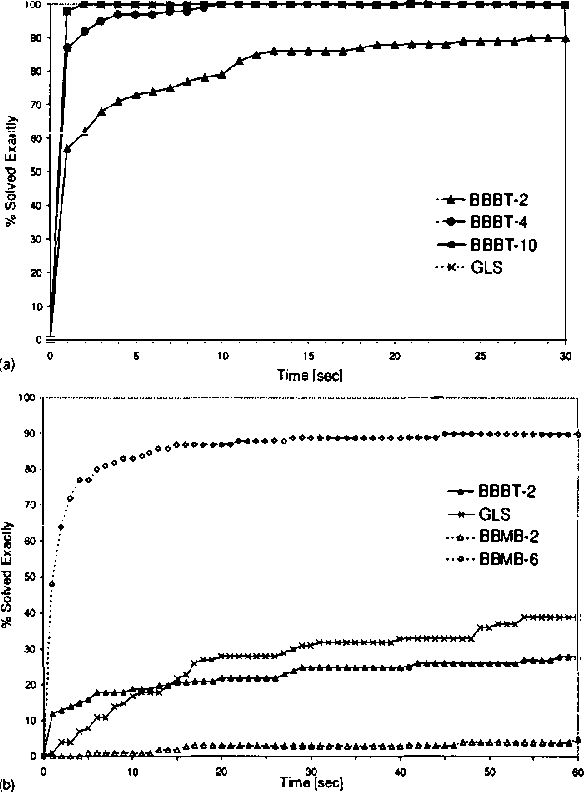
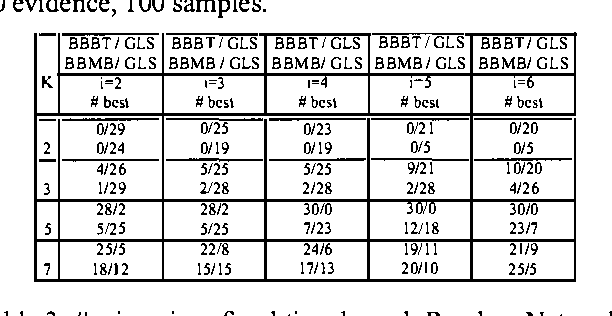
The paper continues the study of partitioning based inference of heuristics for search in the context of solving the Most Probable Explanation task in Bayesian Networks. We compare two systematic Branch and Bound search algorithms, BBBT (for which the heuristic information is constructed during search and allows dynamic variable/value ordering) and its predecessor BBMB (for which the heuristic information is pre-compiled), against a number of popular local search algorithms for the MPE problem. We show empirically that, when viewed as approximation schemes, BBBT/BBMB are superior to all of these best known SLS algorithms, especially when the domain sizes increase beyond 2. This is in contrast with the performance of SLS vs. systematic search on CSP/SAT problems, where SLS often significantly outperforms systematic algorithms. As far as we know, BBBT/BBMB are currently the best performing algorithms for solving the MPE task.

BEEM : Bucket Elimination with External Memory

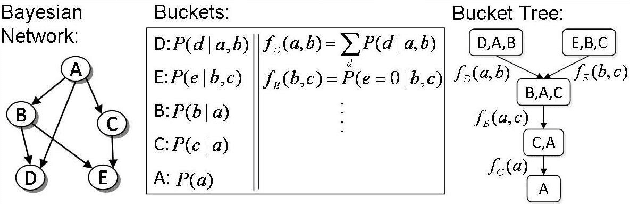
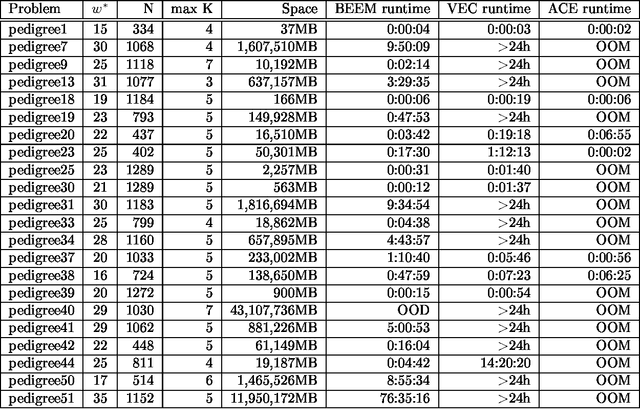
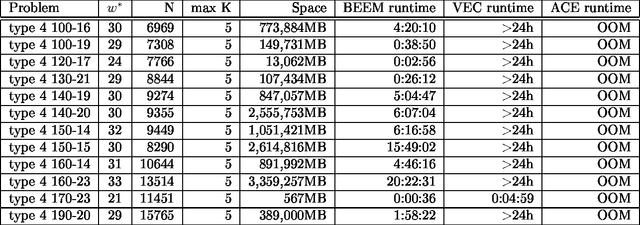
A major limitation of exact inference algorithms for probabilistic graphical models is their extensive memory usage, which often puts real-world problems out of their reach. In this paper we show how we can extend inference algorithms, particularly Bucket Elimination, a special case of cluster (join) tree decomposition, to utilize disk memory. We provide the underlying ideas and show promising empirical results of exactly solving large problems not solvable before.