Generalized Belief Propagation on Tree Robust Structured Region Graphs
Paper and Code
Oct 16, 2012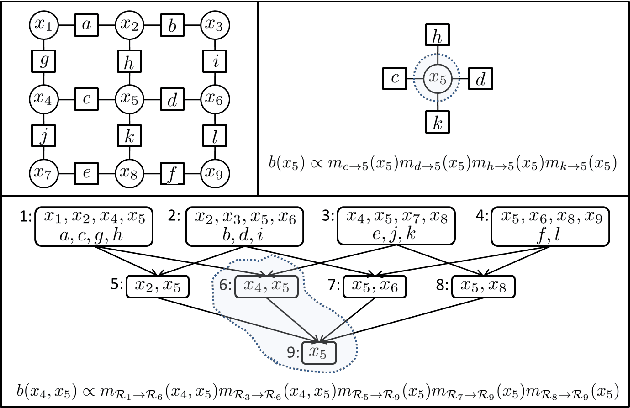
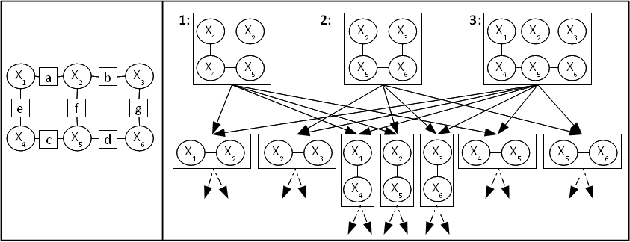
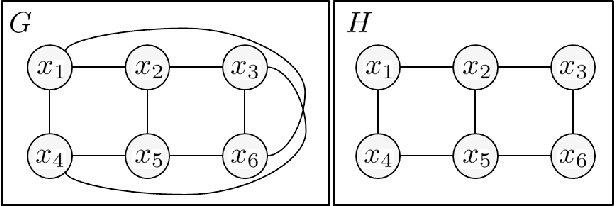
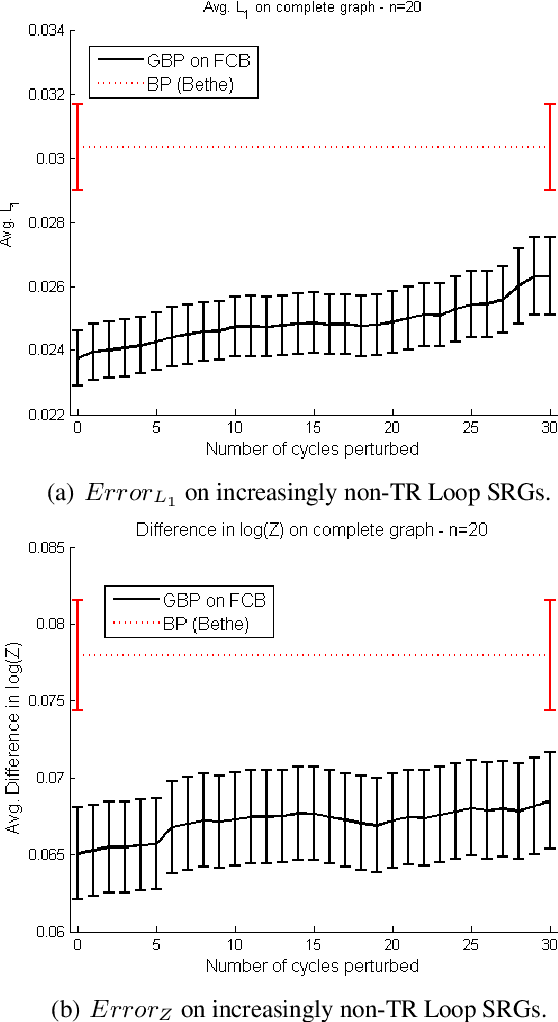
This paper provides some new guidance in the construction of region graphs for Generalized Belief Propagation (GBP). We connect the problem of choosing the outer regions of a LoopStructured Region Graph (SRG) to that of finding a fundamental cycle basis of the corresponding Markov network. We also define a new class of tree-robust Loop-SRG for which GBP on any induced (spanning) tree of the Markov network, obtained by setting to zero the off-tree interactions, is exact. This class of SRG is then mapped to an equivalent class of tree-robust cycle bases on the Markov network. We show that a treerobust cycle basis can be identified by proving that for every subset of cycles, the graph obtained from the edges that participate in a single cycle only, is multiply connected. Using this we identify two classes of tree-robust cycle bases: planar cycle bases and "star" cycle bases. In experiments we show that tree-robustness can be successfully exploited as a design principle to improve the accuracy and convergence of GBP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge