Toward Optimal FDM Toolpath Planning with Monte Carlo Tree Search

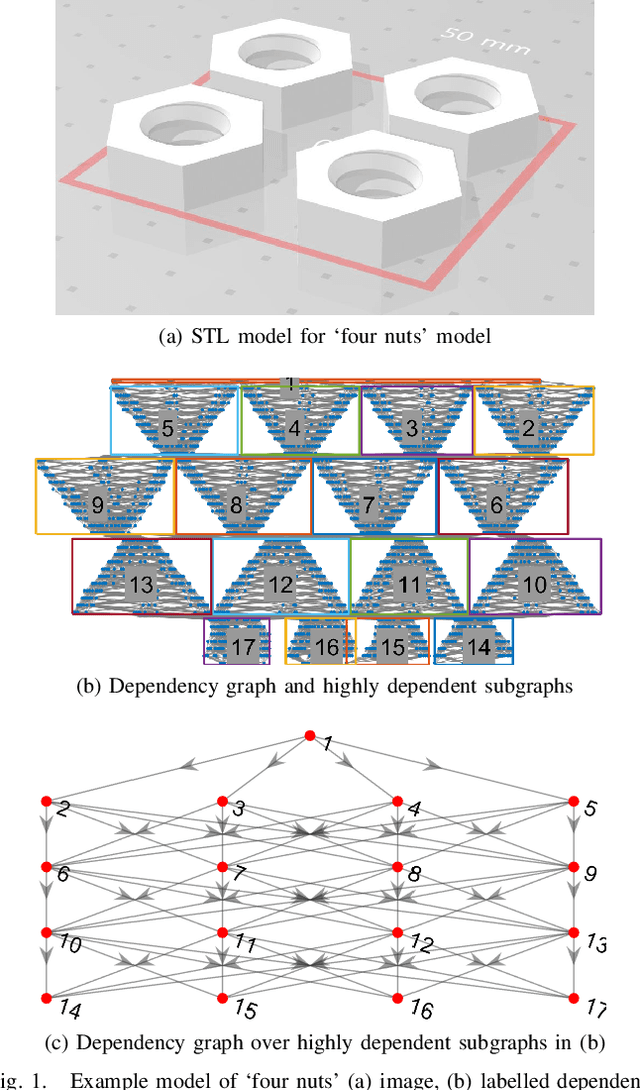
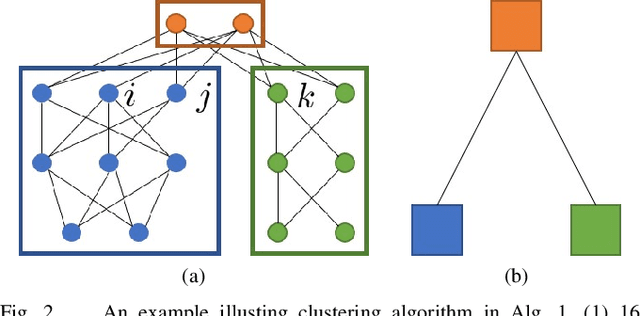
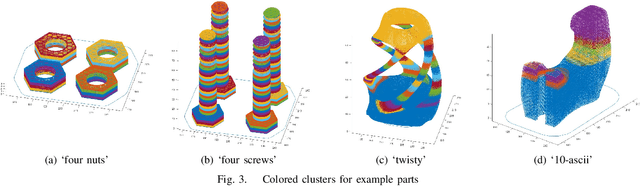
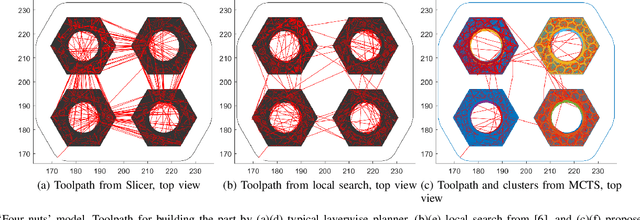
The most widely used methods for toolpath planning in fused deposition 3D printing slice the input model into successive 2D layers in order to construct the toolpath. Unfortunately slicing-based methods can incur a substantial amount of wasted motion (i.e., the extruder is moving while not printing), particularly when features of the model are spatially separated. In recent years we have introduced a new paradigm that characterizes the space of feasible toolpaths using a dependency graph on the input model, along with several algorithms to search this space for toolpaths that optimize objective functions such as wasted motion or print time. A natural question that arises is, under what circumstances can we efficiently compute an optimal toolpath? In this paper, we give an algorithm for computing fused deposition modeling (FDM) toolpaths that utilizes Monte Carlo Tree Search (MCTS), a powerful general-purpose method for navigating large search spaces that is guaranteed to converge to the optimal solution. Under reasonable assumptions on printer geometry that allow us to compress the dependency graph, our MCTS-based algorithm converges to find the optimal toolpath. We validate our algorithm on a dataset of 75 models and show it performs on par with our previous best local search-based algorithm in terms of toolpath quality. In prior work we speculated that the performance of local search was near optimal, and we examine in detail the properties of the models and MCTS executions that lead to better or worse results than local search.

Optimal Time Bounds for Approximate Clustering

Clustering is a fundamental problem in unsupervised learning, and has been studied widely both as a problem of learning mixture models and as an optimization problem. In this paper, we study clustering with respect the emph{k-median} objective function, a natural formulation of clustering in which we attempt to minimize the average distance to cluster centers. One of the main contributions of this paper is a simple but powerful sampling technique that we call emph{successive sampling} that could be of independent interest. We show that our sampling procedure can rapidly identify a small set of points (of size just O(klog{n/k})) that summarize the input points for the purpose of clustering. Using successive sampling, we develop an algorithm for the k-median problem that runs in O(nk) time for a wide range of values of k and is guaranteed, with high probability, to return a solution with cost at most a constant factor times optimal. We also establish a lower bound of Omega(nk) on any randomized constant-factor approximation algorithm for the k-median problem that succeeds with even a negligible (say 1/100) probability. Thus we establish a tight time bound of Theta(nk) for the k-median problem for a wide range of values of k. The best previous upper bound for the problem was O(nk), where the O-notation hides polylogarithmic factors in n and k. The best previous lower bound of O(nk) applied only to deterministic k-median algorithms. While we focus our presentation on the k-median objective, all our upper bounds are valid for the k-means objective as well. In this context our algorithm compares favorably to the widely used k-means heuristic, which requires O(nk) time for just one iteration and provides no useful approximation guarantees.

Adaptive Inference on General Graphical Models

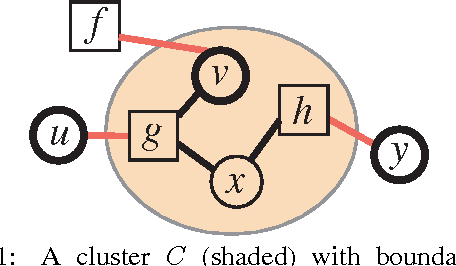
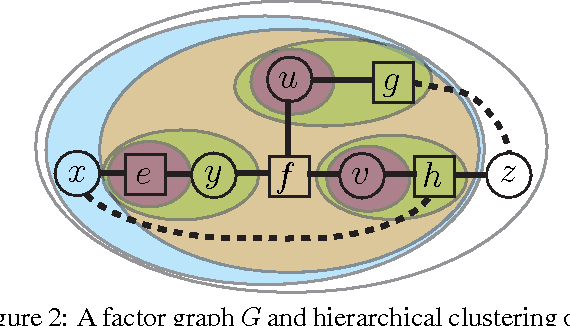
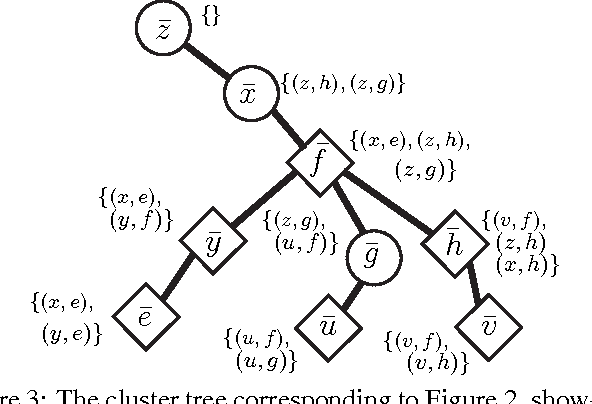
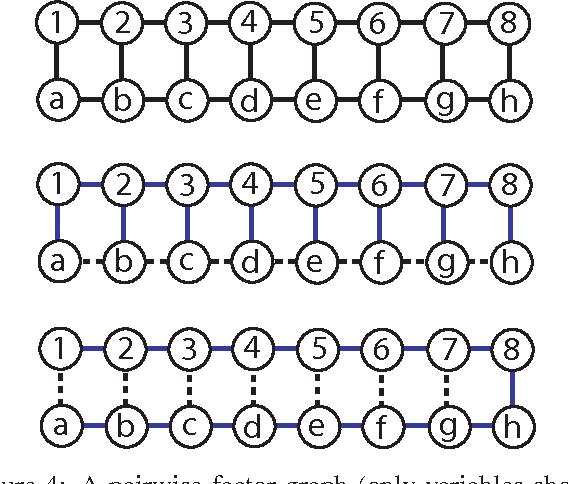
Many algorithms and applications involve repeatedly solving variations of the same inference problem; for example we may want to introduce new evidence to the model or perform updates to conditional dependencies. The goal of adaptive inference is to take advantage of what is preserved in the model and perform inference more rapidly than from scratch. In this paper, we describe techniques for adaptive inference on general graphs that support marginal computation and updates to the conditional probabilities and dependencies in logarithmic time. We give experimental results for an implementation of our algorithm, and demonstrate its potential performance benefit in the study of protein structure.