Multilinear Wavelets: A Statistical Shape Space for Human Faces

We present a statistical model for $3$D human faces in varying expression, which decomposes the surface of the face using a wavelet transform, and learns many localized, decorrelated multilinear models on the resulting coefficients. Using this model we are able to reconstruct faces from noisy and occluded $3$D face scans, and facial motion sequences. Accurate reconstruction of face shape is important for applications such as tele-presence and gaming. The localized and multi-scale nature of our model allows for recovery of fine-scale detail while retaining robustness to severe noise and occlusion, and is computationally efficient and scalable. We validate these properties experimentally on challenging data in the form of static scans and motion sequences. We show that in comparison to a global multilinear model, our model better preserves fine detail and is computationally faster, while in comparison to a localized PCA model, our model better handles variation in expression, is faster, and allows us to fix identity parameters for a given subject.

Estimation of Human Body Shape and Posture Under Clothing

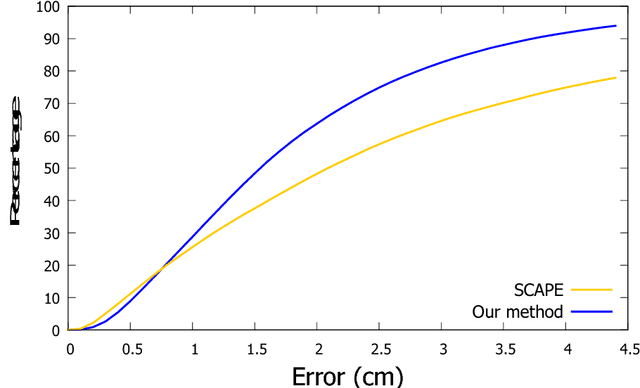
Estimating the body shape and posture of a dressed human subject in motion represented as a sequence of (possibly incomplete) 3D meshes is important for virtual change rooms and security. To solve this problem, statistical shape spaces encoding human body shape and posture variations are commonly used to constrain the search space for the shape estimate. In this work, we propose a novel method that uses a posture-invariant shape space to model body shape variation combined with a skeleton-based deformation to model posture variation. Our method can estimate the body shape and posture of both static scans and motion sequences of dressed human body scans. In case of motion sequences, our method takes advantage of motion cues to solve for a single body shape estimate along with a sequence of posture estimates. We apply our approach to both static scans and motion sequences and demonstrate that using our method, higher fitting accuracy is achieved than when using a variant of the popular SCAPE model as statistical model.

Review of Statistical Shape Spaces for 3D Data with Comparative Analysis for Human Faces

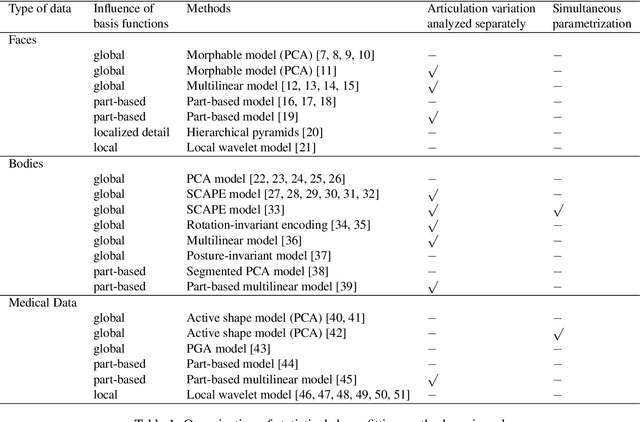
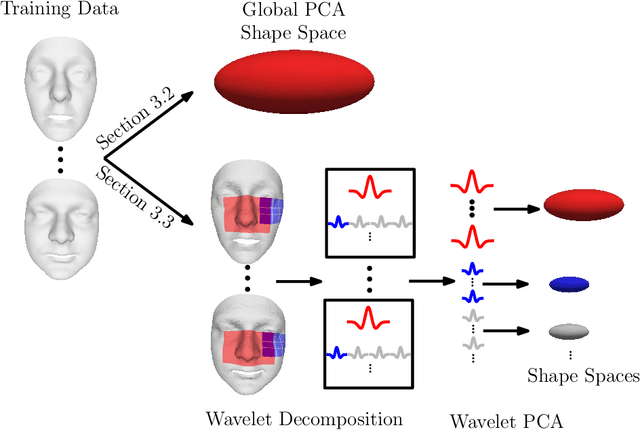
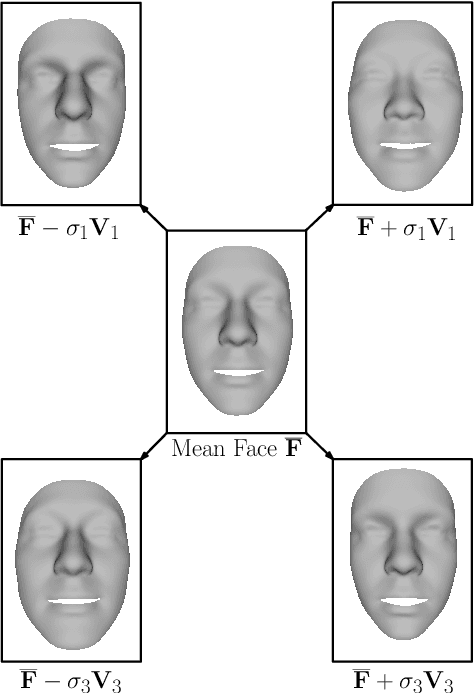
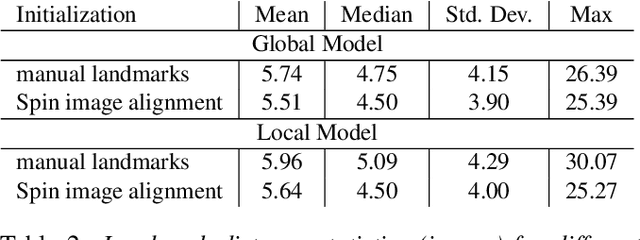
With systems for acquiring 3D surface data being evermore commonplace, it has become important to reliably extract specific shapes from the acquired data. In the presence of noise and occlusions, this can be done through the use of statistical shape models, which are learned from databases of clean examples of the shape in question. In this paper, we review, analyze and compare different statistical models: from those that analyze the variation in geometry globally to those that analyze the variation in geometry locally. We first review how different types of models have been used in the literature, then proceed to define the models and analyze them theoretically, in terms of both their statistical and computational aspects. We then perform extensive experimental comparison on the task of model fitting, and give intuition about which type of model is better for a few applications. Due to the wide availability of databases of high-quality data, we use the human face as the specific shape we wish to extract from corrupted data.

A Low-Dimensional Representation for Robust Partial Isometric Correspondences Computation

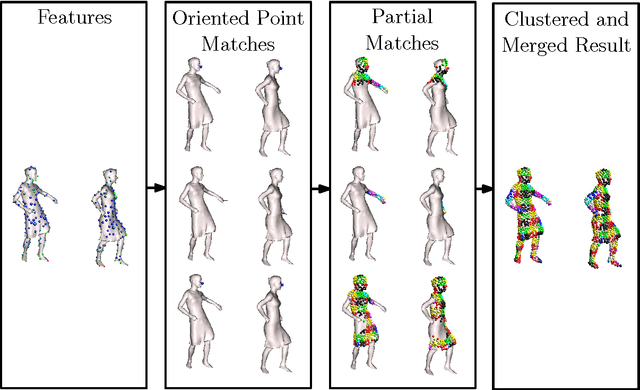
Intrinsic isometric shape matching has become the standard approach for pose invariant correspondence estimation among deformable shapes. Most existing approaches assume global consistency, i.e., the metric structure of the whole manifold must not change significantly. While global isometric matching is well understood, only a few heuristic solutions are known for partial matching. Partial matching is particularly important for robustness to topological noise (incomplete data and contacts), which is a common problem in real-world 3D scanner data. In this paper, we introduce a new approach to partial, intrinsic isometric matching. Our method is based on the observation that isometries are fully determined by purely local information: a map of a single point and its tangent space fixes an isometry for both global and the partial maps. From this idea, we develop a new representation for partial isometric maps based on equivalence classes of correspondences between pairs of points and their tangent spaces. From this, we derive a local propagation algorithm that find such mappings efficiently. In contrast to previous heuristics based on RANSAC or expectation maximization, our method is based on a simple and sound theoretical model and fully deterministic. We apply our approach to register partial point clouds and compare it to the state-of-the-art methods, where we obtain significant improvements over global methods for real-world data and stronger guarantees than previous heuristic partial matching algorithms.