Ahmad-Reza Ehyaei
Designing Ambiguity Sets for Distributionally Robust Optimization Using Structural Causal Optimal Transport
Oct 01, 2025Abstract:Distributionally robust optimization tackles out-of-sample issues like overfitting and distribution shifts by adopting an adversarial approach over a range of possible data distributions, known as the ambiguity set. To balance conservatism and accuracy, these sets must include realistic probability distributions by leveraging information from the nominal distribution. Assuming that nominal distributions arise from a structural causal model with a directed acyclic graph $\mathcal{G}$ and structural equations, previous methods such as adapted and $\mathcal{G}$-causal optimal transport have only utilized causal graph information in designing ambiguity sets. In this work, we propose incorporating structural equations, which include causal graph information, to enhance ambiguity sets, resulting in more realistic distributions. We introduce structural causal optimal transport and its associated ambiguity set, demonstrating their advantages and connections to previous methods. A key benefit of our approach is a relaxed version, where a regularization term replaces the complex causal constraints, enabling an efficient algorithm via difference-of-convex programming to solve structural causal optimal transport. We also show that when structural information is absent and must be estimated, our approach remains effective and provides finite sample guarantees. Lastly, we address the radius of ambiguity sets, illustrating how our method overcomes the curse of dimensionality in optimal transport problems, achieving faster shrinkage with dimension-free order.
Collective Counterfactual Explanations via Optimal Transport
Feb 07, 2024Abstract:Counterfactual explanations provide individuals with cost-optimal actions that can alter their labels to desired classes. However, if substantial instances seek state modification, such individual-centric methods can lead to new competitions and unanticipated costs. Furthermore, these recommendations, disregarding the underlying data distribution, may suggest actions that users perceive as outliers. To address these issues, our work proposes a collective approach for formulating counterfactual explanations, with an emphasis on utilizing the current density of the individuals to inform the recommended actions. Our problem naturally casts as an optimal transport problem. Leveraging the extensive literature on optimal transport, we illustrate how this collective method improves upon the desiderata of classical counterfactual explanations. We support our proposal with numerical simulations, illustrating the effectiveness of the proposed approach and its relation to classic methods.
Causal Fair Metric: Bridging Causality, Individual Fairness, and Adversarial Robustness
Oct 30, 2023Abstract:Adversarial perturbation is used to expose vulnerabilities in machine learning models, while the concept of individual fairness aims to ensure equitable treatment regardless of sensitive attributes. Despite their initial differences, both concepts rely on metrics to generate similar input data instances. These metrics should be designed to align with the data's characteristics, especially when it is derived from causal structure and should reflect counterfactuals proximity. Previous attempts to define such metrics often lack general assumptions about data or structural causal models. In this research, we introduce a causal fair metric formulated based on causal structures that encompass sensitive attributes. For robustness analysis, the concept of protected causal perturbation is presented. Additionally, we delve into metric learning, proposing a method for metric estimation and deployment in real-world problems. The introduced metric has applications in the fields adversarial training, fair learning, algorithmic recourse, and causal reinforcement learning.
Causal Adversarial Perturbations for Individual Fairness and Robustness in Heterogeneous Data Spaces
Aug 17, 2023Abstract:As responsible AI gains importance in machine learning algorithms, properties such as fairness, adversarial robustness, and causality have received considerable attention in recent years. However, despite their individual significance, there remains a critical gap in simultaneously exploring and integrating these properties. In this paper, we propose a novel approach that examines the relationship between individual fairness, adversarial robustness, and structural causal models in heterogeneous data spaces, particularly when dealing with discrete sensitive attributes. We use causal structural models and sensitive attributes to create a fair metric and apply it to measure semantic similarity among individuals. By introducing a novel causal adversarial perturbation and applying adversarial training, we create a new regularizer that combines individual fairness, causality, and robustness in the classifier. Our method is evaluated on both real-world and synthetic datasets, demonstrating its effectiveness in achieving an accurate classifier that simultaneously exhibits fairness, adversarial robustness, and causal awareness.
Robustness Implies Fairness in Causal Algorithmic Recourse
Feb 11, 2023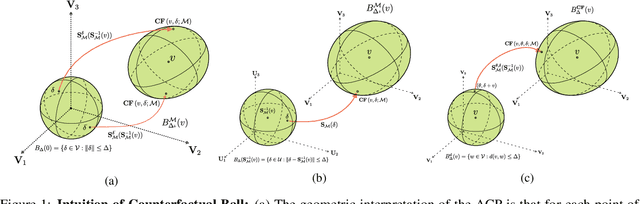

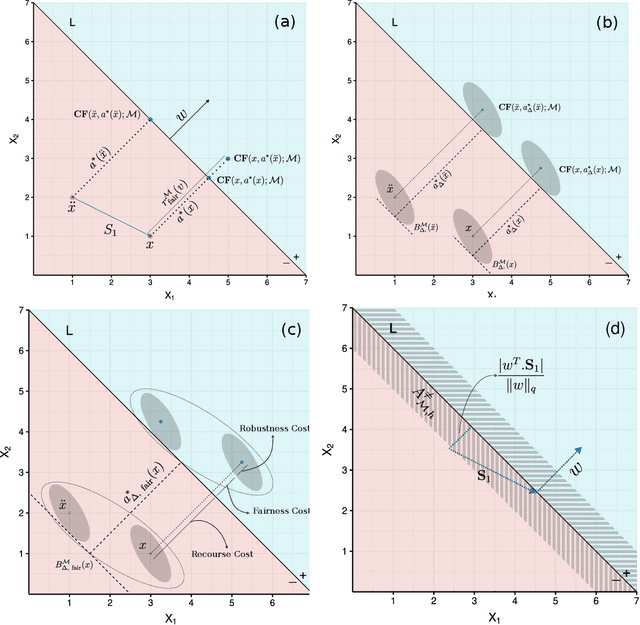

Abstract:Algorithmic recourse aims to disclose the inner workings of the black-box decision process in situations where decisions have significant consequences, by providing recommendations to empower beneficiaries to achieve a more favorable outcome. To ensure an effective remedy, suggested interventions must not only be low-cost but also robust and fair. This goal is accomplished by providing similar explanations to individuals who are alike. This study explores the concept of individual fairness and adversarial robustness in causal algorithmic recourse and addresses the challenge of achieving both. To resolve the challenges, we propose a new framework for defining adversarially robust recourse. The new setting views the protected feature as a pseudometric and demonstrates that individual fairness is a special case of adversarial robustness. Finally, we introduce the fair robust recourse problem to achieve both desirable properties and show how it can be satisfied both theoretically and empirically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge