Analysis of Bootstrap and Subsampling in High-dimensional Regularized Regression

We investigate popular resampling methods for estimating the uncertainty of statistical models, such as subsampling, bootstrap and the jackknife, and their performance in high-dimensional supervised regression tasks. We provide a tight asymptotic description of the biases and variances estimated by these methods in the context of generalized linear models, such as ridge and logistic regression, taking the limit where the number of samples $n$ and dimension $d$ of the covariates grow at a comparable fixed rate $\alpha\!=\! n/d$. Our findings are three-fold: i) resampling methods are fraught with problems in high dimensions and exhibit the double-descent-like behavior typical of these situations; ii) only when $\alpha$ is large enough do they provide consistent and reliable error estimations (we give convergence rates); iii) in the over-parametrized regime $\alpha\!<\!1$ relevant to modern machine learning practice, their predictions are not consistent, even with optimal regularization.

Lower Bounds on the Bayesian Risk via Information Measures

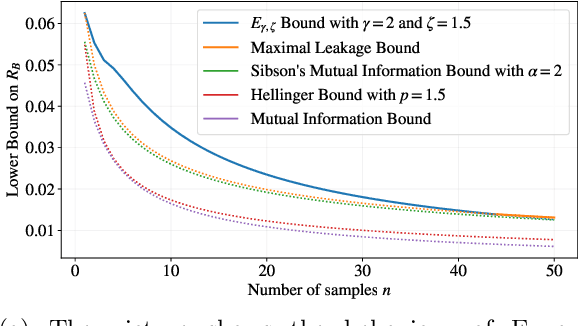
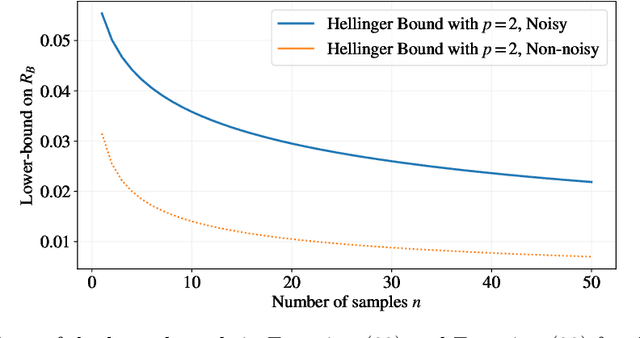
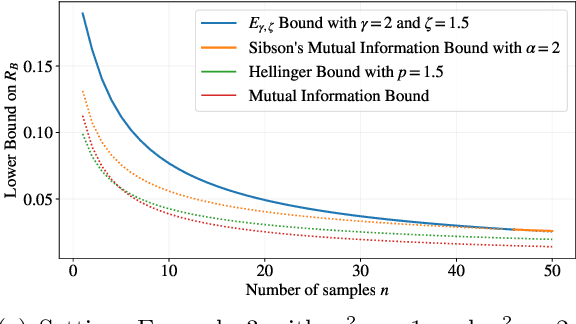
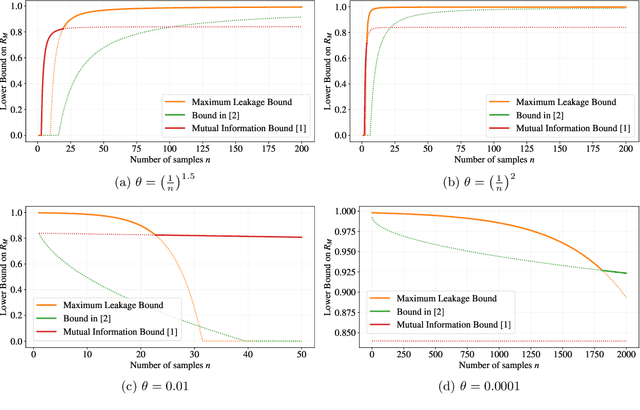
This paper focuses on parameter estimation and introduces a new method for lower bounding the Bayesian risk. The method allows for the use of virtually \emph{any} information measure, including R\'enyi's $\alpha$, $\varphi$-Divergences, and Sibson's $\alpha$-Mutual Information. The approach considers divergences as functionals of measures and exploits the duality between spaces of measures and spaces of functions. In particular, we show that one can lower bound the risk with any information measure by upper bounding its dual via Markov's inequality. We are thus able to provide estimator-independent impossibility results thanks to the Data-Processing Inequalities that divergences satisfy. The results are then applied to settings of interest involving both discrete and continuous parameters, including the ``Hide-and-Seek'' problem, and compared to the state-of-the-art techniques. An important observation is that the behaviour of the lower bound in the number of samples is influenced by the choice of the information measure. We leverage this by introducing a new divergence inspired by the ``Hockey-Stick'' Divergence, which is demonstrated empirically to provide the largest lower-bound across all considered settings. If the observations are subject to privatisation, stronger impossibility results can be obtained via Strong Data-Processing Inequalities. The paper also discusses some generalisations and alternative directions.