A Survey on the Densest Subgraph Problem and its Variants

The Densest Subgraph Problem requires to find, in a given graph, a subset of vertices whose induced subgraph maximizes a measure of density. The problem has received a great deal of attention in the algorithmic literature over the last five decades, with many variants proposed and many applications built on top of this basic definition. Recent years have witnessed a revival of research interest on this problem with several interesting contributions, including some groundbreaking results, published in 2022 and 2023. This survey provides a deep overview of the fundamental results and an exhaustive coverage of the many variants proposed in the literature, with a special attention on the most recent results. The survey also presents a comprehensive overview of applications and discusses some interesting open problems for this evergreen research topic.

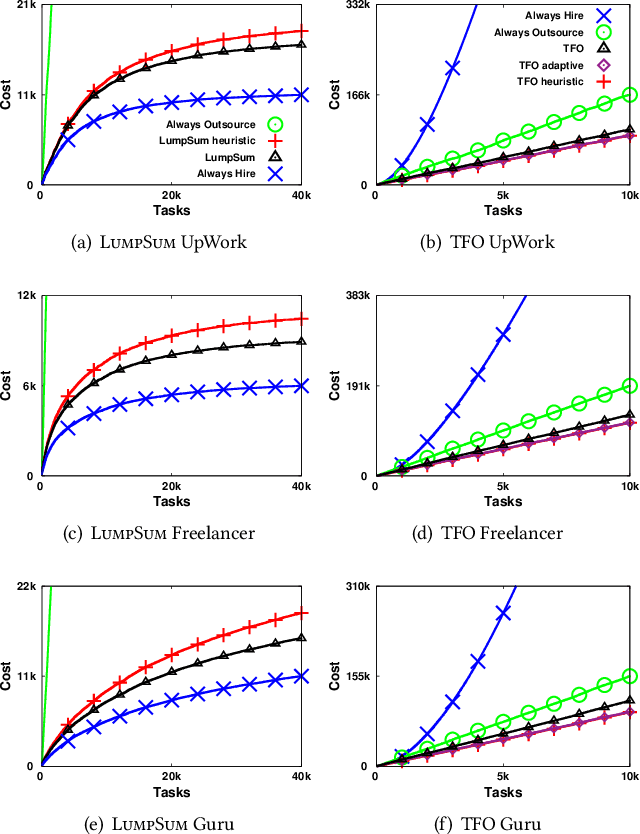
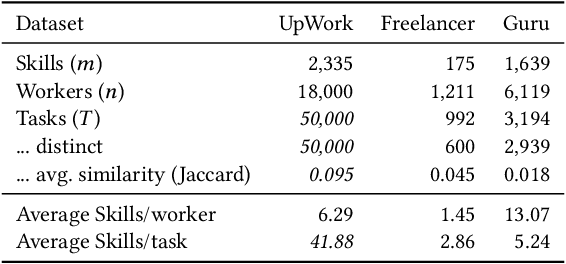
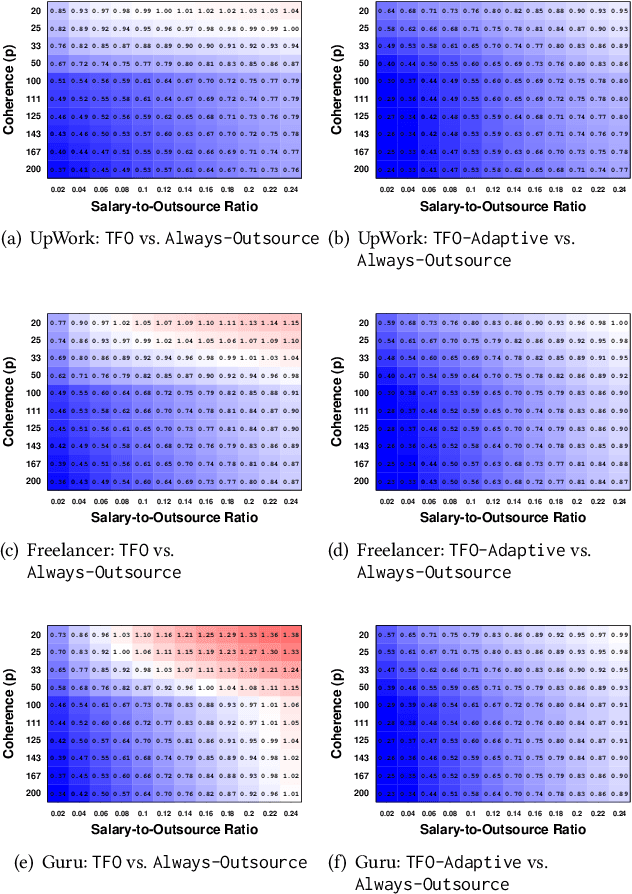
Algorithms for Hiring and Outsourcing in the Online Labor Market

Although freelancing work has grown substantially in recent years, in part facilitated by a number of online labor marketplaces, (e.g., Guru, Freelancer, Amazon Mechanical Turk), traditional forms of "in-sourcing" work continue being the dominant form of employment. This means that, at least for the time being, freelancing and salaried employment will continue to co-exist. In this paper, we provide algorithms for outsourcing and hiring workers in a general setting, where workers form a team and contribute different skills to perform a task. We call this model team formation with outsourcing. In our model, tasks arrive in an online fashion: neither the number nor the composition of the tasks is known a-priori. At any point in time, there is a team of hired workers who receive a fixed salary independently of the work they perform. This team is dynamic: new members can be hired and existing members can be fired, at some cost. Additionally, some parts of the arriving tasks can be outsourced and thus completed by non-team members, at a premium. Our contribution is an efficient online cost-minimizing algorithm for hiring and firing team members and outsourcing tasks. We present theoretical bounds obtained using a primal-dual scheme proving that our algorithms have a logarithmic competitive approximation ratio. We complement these results with experiments using semi-synthetic datasets based on actual task requirements and worker skills from three large online labor marketplaces.

Algorithms for Fair Team Formation in Online Labour Marketplaces

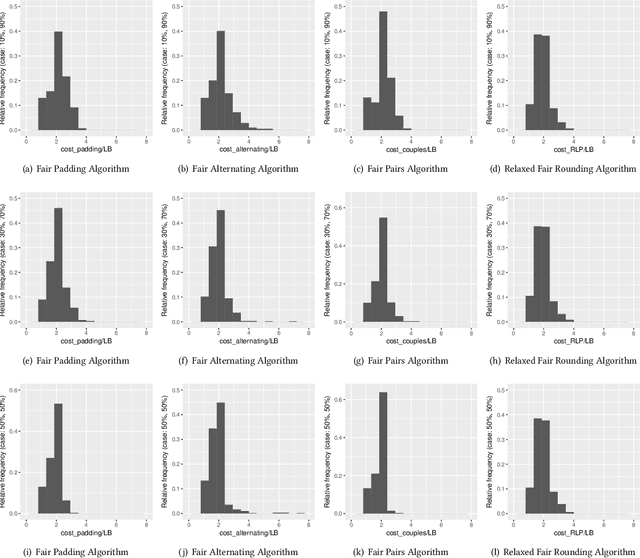
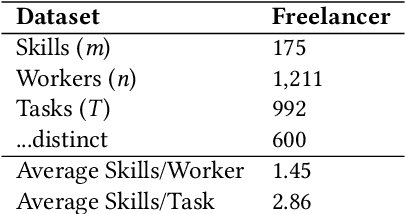
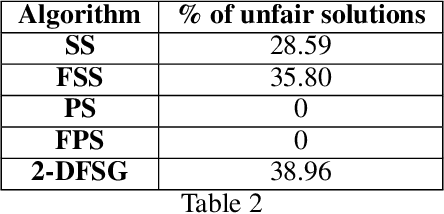
As freelancing work keeps on growing almost everywhere due to a sharp decrease in communication costs and to the widespread of Internet-based labour marketplaces (e.g., guru.com, feelancer.com, mturk.com, upwork.com), many researchers and practitioners have started exploring the benefits of outsourcing and crowdsourcing. Since employers often use these platforms to find a group of workers to complete a specific task, researchers have focused their efforts on the study of team formation and matching algorithms and on the design of effective incentive schemes. Nevertheless, just recently, several concerns have been raised on possibly unfair biases introduced through the algorithms used to carry out these selection and matching procedures. For this reason, researchers have started studying the fairness of algorithms related to these online marketplaces, looking for intelligent ways to overcome the algorithmic bias that frequently arises. Broadly speaking, the aim is to guarantee that, for example, the process of hiring workers through the use of machine learning and algorithmic data analysis tools does not discriminate, even unintentionally, on grounds of nationality or gender. In this short paper, we define the Fair Team Formation problem in the following way: given an online labour marketplace where each worker possesses one or more skills, and where all workers are divided into two or more not overlapping classes (for examples, men and women), we want to design an algorithm that is able to find a team with all the skills needed to complete a given task, and that has the same number of people from all classes. We provide inapproximability results for the Fair Team Formation problem together with four algorithms for the problem itself. We also tested the effectiveness of our algorithmic solutions by performing experiments using real data from an online labor marketplace.

Principal Fairness: \\ Removing Bias via Projections

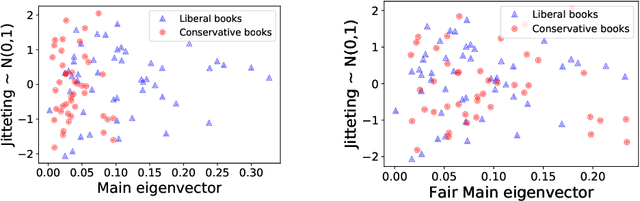
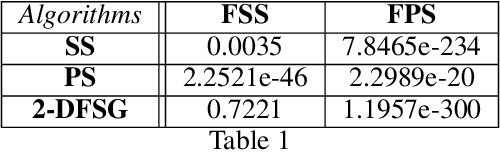
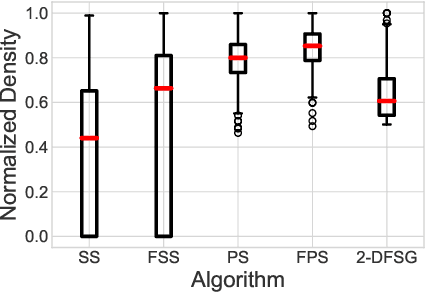
Reducing hidden bias in the data and ensuring fairness in algorithmic data analysis has recently received significant attention. We complement several recent papers in this line of research by introducing a general method to reduce bias in the data through random projections in a ``fair'' subspace. We apply this method to densest subgraph and $k$-means. For densest subgraph, our approach based on fair projections allows to recover both theoretically and empirically an almost optimal, fair, dense subgraph hidden in the input data. We also show that, under the small set expansion hypothesis, approximating this problem beyond a factor of $2$ is NP-hard and we show a polynomial time algorithm with a matching approximation bound. We further apply our method to $k$-means. In a previous paper, Chierichetti et al.~[NIPS 2017] showed that problems such as $k$-means can be approximated up to a constant factor while ensuring that none of two protected class (e.g., gender, ethnicity) is disparately impacted. We show that fair projections generalize the concept of fairlet introduced by Chierichietti et al. to any number of protected attributes and improve empirically the quality of the resulting clustering. We also present the first constant-factor approximation for an arbitrary number of protected attributes thus settling an open problem recently addressed in several works.