Aditya Siripuram
Exploring the Limitations of Structured Orthogonal Dictionary Learning
Jan 25, 2025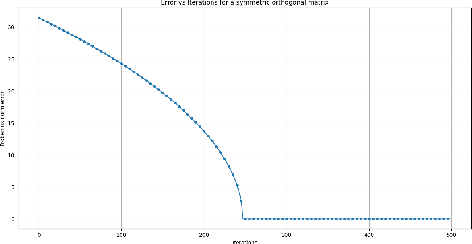

Abstract:This work is motivated by recent applications of structured dictionary learning, in particular when the dictionary is assumed to be the product of a few Householder atoms. We investigate the following two problems: 1) How do we approximate an orthogonal matrix $\mathbf{V}$ with a product of a specified number of Householder matrices, and 2) How many samples are required to learn a structured (Householder) dictionary from data? For 1) we discuss an algorithm that decomposes $\mathbf{V}$ as a product of a specified number of Householder matrices. We see that the algorithm outputs the decomposition when it exists, and give bounds on the approximation error of the algorithm when such a decomposition does not exist. For 2) given data $\mathbf{Y}=\mathbf{HX}$, we show that when assuming a binary coefficient matrix $\mathbf{X}$, the structured (Householder) dictionary learning problem can be solved with just $2$ samples (columns) in $\mathbf{Y}$.
Fast Structured Orthogonal Dictionary Learning using Householder Reflections
Sep 13, 2024Abstract:In this paper, we propose and investigate algorithms for the structured orthogonal dictionary learning problem. First, we investigate the case when the dictionary is a Householder matrix. We give sample complexity results and show theoretically guaranteed approximate recovery (in the $l_{\infty}$ sense) with optimal computational complexity. We then attempt to generalize these techniques when the dictionary is a product of a few Householder matrices. We numerically validate these techniques in the sample-limited setting to show performance similar to or better than existing techniques while having much improved computational complexity.
Joint Data Inpainting and Graph Learning via Unrolled Neural Networks
Jul 16, 2024Abstract:Given partial measurements of a time-varying graph signal, we propose an algorithm to simultaneously estimate both the underlying graph topology and the missing measurements. The proposed algorithm operates by training an interpretable neural network, designed from the unrolling framework. The proposed technique can be used both as a graph learning and a graph signal reconstruction algorithm. This work enhances prior work in graph signal reconstruction by allowing the underlying graph to be unknown; and also builds on prior work in graph learning by tailoring the learned graph to the signal reconstruction task.
Efficient Matrix Factorization Via Householder Reflections
May 13, 2024Abstract:Motivated by orthogonal dictionary learning problems, we propose a novel method for matrix factorization, where the data matrix $\mathbf{Y}$ is a product of a Householder matrix $\mathbf{H}$ and a binary matrix $\mathbf{X}$. First, we show that the exact recovery of the factors $\mathbf{H}$ and $\mathbf{X}$ from $\mathbf{Y}$ is guaranteed with $\Omega(1)$ columns in $\mathbf{Y}$ . Next, we show approximate recovery (in the $l\infty$ sense) can be done in polynomial time($O(np)$) with $\Omega(\log n)$ columns in $\mathbf{Y}$ . We hope the techniques in this work help in developing alternate algorithms for orthogonal dictionary learning.
Numerical Stability of DFT Computation for Signals with Structured Support
Jan 29, 2024Abstract:We consider the problem of building numerically stable algorithms for computing Discrete Fourier Transform (DFT) of $N$- length signals with known frequency support of size $k$. A typical algorithm, in this case, would involve solving (possibly poorly conditioned) system of equations, causing numerical instability. When $N$ is a power of 2, and the frequency support is a random subset of $\mathbb{Z}_N$, we provide an algorithm that has (a possibly optimal) $O(k \log k)$ complexity to compute the DFT while solving system of equations that are $O(1)$ in size.
Fast DFT Computation for Signals with Structured Support
Nov 28, 2022



Abstract:Suppose an $N-$length signal has known frequency support of size $k$. Given sample access to this signal, how fast can we compute the DFT? The answer to this question depends on the structure of the frequency support. We first identify some frequency supports for which (an ideal) $O(k \log k)$ complexity is achievable, referred to as homogeneous sets. We give a generalization of radix-2 that enables $O(k\log k)$ computation of signals with homogeneous frequency support. Using homogeneous sets as building blocks, we construct more complicated support structures for which the complexity of $O(k\log k)$ is achievable. We also investigate the relationship of DFT computation with additive structure in the support and provide partial converses.
Perceptually Guided Adversarial Perturbations
Jun 24, 2021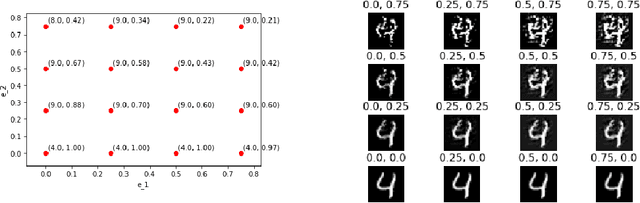

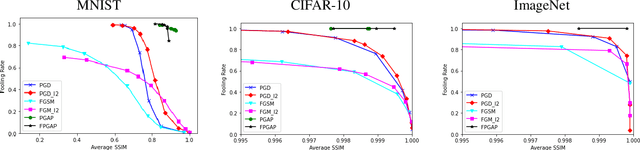
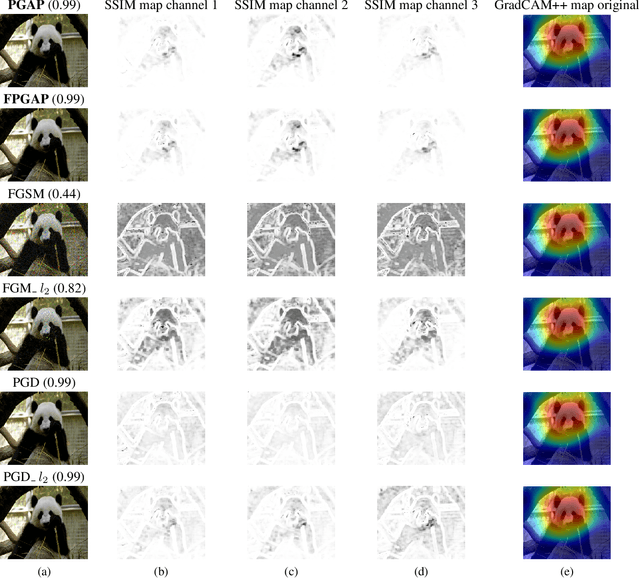
Abstract:It is well known that carefully crafted imperceptible perturbations can cause state-of-the-art deep learning classification models to misclassify. Understanding and analyzing these adversarial perturbations play a crucial role in the design of robust convolutional neural networks. However, the reasons for the existence of adversarial perturbations and their mechanics are not well understood. In this work, we attempt to systematically answer the following question: do imperceptible adversarial perturbations focus on changing the regions of the image that are important for classification? Most current methods use $l_p$ distance to generate and characterize the imperceptibility of the adversarial perturbations. However, since $l_p$ distances only measure the pixel to pixel distances and do not consider the structure in the image, these methods do not provide a satisfactory answer to the above question. To address this issue, we propose a novel framework for generating adversarial perturbations by explicitly incorporating a ``perceptual quality ball" constraint in our formulation. Specifically, we pose the adversarial example generation problem as a tractable convex optimization problem, with constraints taken from a mathematically amenable variant of the popular SSIM index. We show that the perturbations generated by the proposed method result in a high fooling rate with minimal impact on perceptual quality compared to the norm bounded adversarial perturbations. Further, through SSIM maps, we show that the perceptually guided perturbations introduce changes specifically in the regions that contribute to classification decisions. We use networks trained on MNIST and CIFAR-10 datasets quantitative analysis, and MobileNetV2 trained on the ImageNet dataset for further qualitative analysis.
Computing the Discrete Fourier Transform of signals with spectral frequency support
Feb 24, 2021

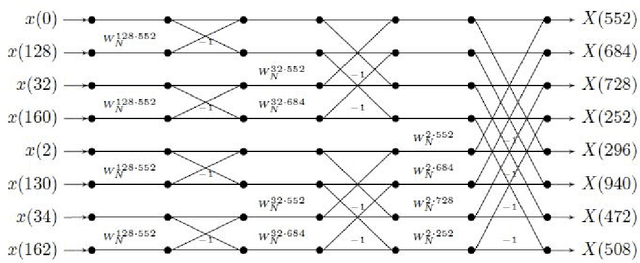
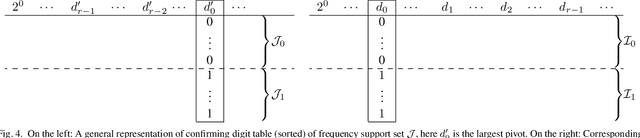
Abstract:We consider the problem of finding the Discrete Fourier Transform (DFT) of $N-$ length signals with known frequency support of size $k$. When $N$ is a power of 2 and the frequency support is a spectral set, we provide an $O(k \log k)$ algorithm to compute the DFT. Our algorithm uses some recent characterizations of spectral sets and is a generalization of the standard radix-2 algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge