Perceptually Guided Adversarial Perturbations

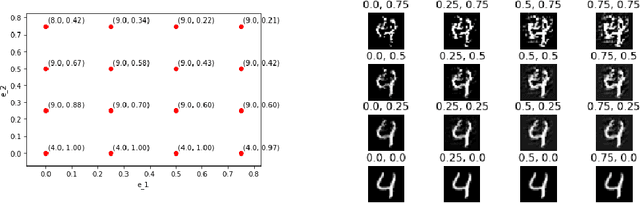
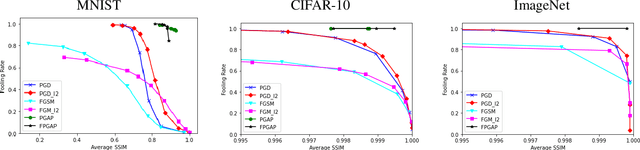
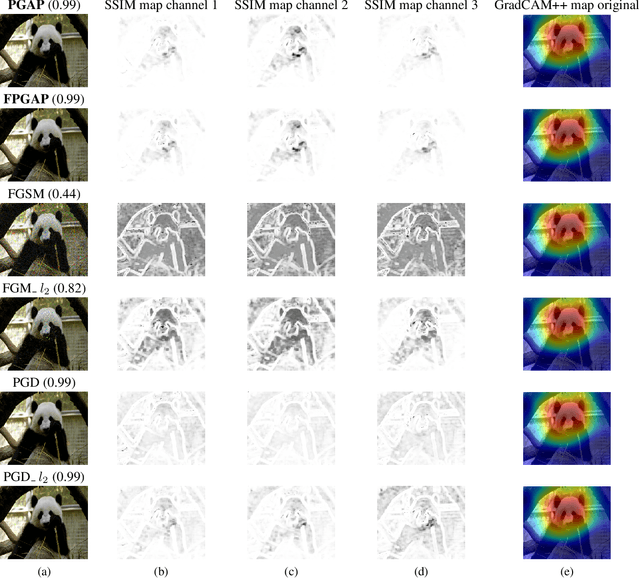
It is well known that carefully crafted imperceptible perturbations can cause state-of-the-art deep learning classification models to misclassify. Understanding and analyzing these adversarial perturbations play a crucial role in the design of robust convolutional neural networks. However, the reasons for the existence of adversarial perturbations and their mechanics are not well understood. In this work, we attempt to systematically answer the following question: do imperceptible adversarial perturbations focus on changing the regions of the image that are important for classification? Most current methods use $l_p$ distance to generate and characterize the imperceptibility of the adversarial perturbations. However, since $l_p$ distances only measure the pixel to pixel distances and do not consider the structure in the image, these methods do not provide a satisfactory answer to the above question. To address this issue, we propose a novel framework for generating adversarial perturbations by explicitly incorporating a ``perceptual quality ball" constraint in our formulation. Specifically, we pose the adversarial example generation problem as a tractable convex optimization problem, with constraints taken from a mathematically amenable variant of the popular SSIM index. We show that the perturbations generated by the proposed method result in a high fooling rate with minimal impact on perceptual quality compared to the norm bounded adversarial perturbations. Further, through SSIM maps, we show that the perceptually guided perturbations introduce changes specifically in the regions that contribute to classification decisions. We use networks trained on MNIST and CIFAR-10 datasets quantitative analysis, and MobileNetV2 trained on the ImageNet dataset for further qualitative analysis.

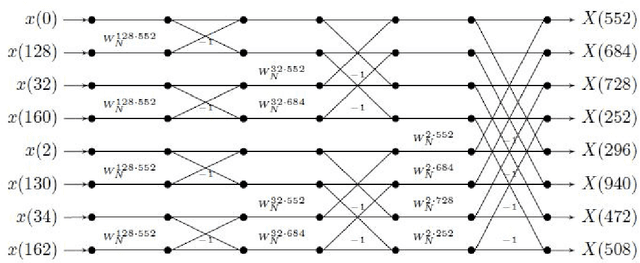
Computing the Discrete Fourier Transform of signals with spectral frequency support

We consider the problem of finding the Discrete Fourier Transform (DFT) of $N-$ length signals with known frequency support of size $k$. When $N$ is a power of 2 and the frequency support is a spectral set, we provide an $O(k \log k)$ algorithm to compute the DFT. Our algorithm uses some recent characterizations of spectral sets and is a generalization of the standard radix-2 algorithm.