Computing the Discrete Fourier Transform of signals with spectral frequency support

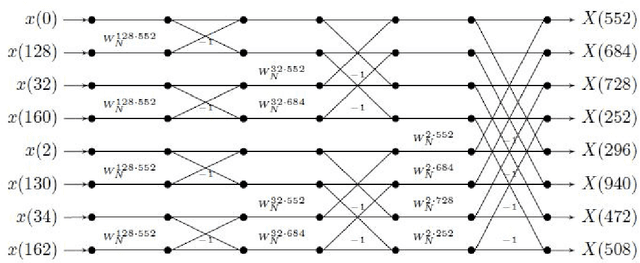
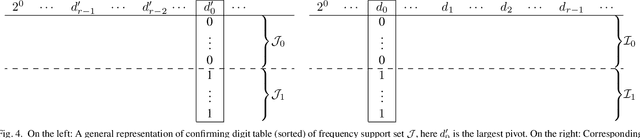
We consider the problem of finding the Discrete Fourier Transform (DFT) of $N-$ length signals with known frequency support of size $k$. When $N$ is a power of 2 and the frequency support is a spectral set, we provide an $O(k \log k)$ algorithm to compute the DFT. Our algorithm uses some recent characterizations of spectral sets and is a generalization of the standard radix-2 algorithm.