Numerical Stability of DFT Computation for Signals with Structured Support

We consider the problem of building numerically stable algorithms for computing Discrete Fourier Transform (DFT) of $N$- length signals with known frequency support of size $k$. A typical algorithm, in this case, would involve solving (possibly poorly conditioned) system of equations, causing numerical instability. When $N$ is a power of 2, and the frequency support is a random subset of $\mathbb{Z}_N$, we provide an algorithm that has (a possibly optimal) $O(k \log k)$ complexity to compute the DFT while solving system of equations that are $O(1)$ in size.

Fast DFT Computation for Signals with Structured Support

Suppose an $N-$length signal has known frequency support of size $k$. Given sample access to this signal, how fast can we compute the DFT? The answer to this question depends on the structure of the frequency support. We first identify some frequency supports for which (an ideal) $O(k \log k)$ complexity is achievable, referred to as homogeneous sets. We give a generalization of radix-2 that enables $O(k\log k)$ computation of signals with homogeneous frequency support. Using homogeneous sets as building blocks, we construct more complicated support structures for which the complexity of $O(k\log k)$ is achievable. We also investigate the relationship of DFT computation with additive structure in the support and provide partial converses.

A Note on the Convolution of Circle Impulses

We present a formula for the convolution $\delta_{C_1}*\delta_{C_2}$ of two circle impulses. The derivation uses a classical addition theorem for Bessel functions.

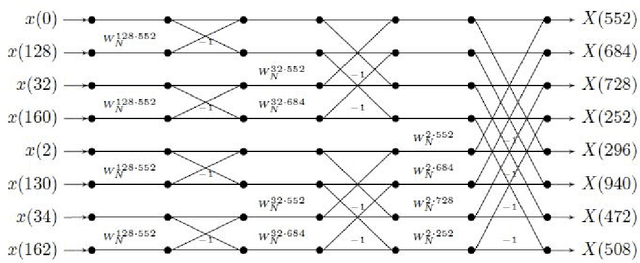
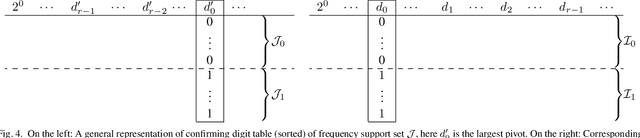
Computing the Discrete Fourier Transform of signals with spectral frequency support

We consider the problem of finding the Discrete Fourier Transform (DFT) of $N-$ length signals with known frequency support of size $k$. When $N$ is a power of 2 and the frequency support is a spectral set, we provide an $O(k \log k)$ algorithm to compute the DFT. Our algorithm uses some recent characterizations of spectral sets and is a generalization of the standard radix-2 algorithm.