Aditya Kashi
Learning the boundary-to-domain mapping using Lifting Product Fourier Neural Operators for partial differential equations
Jun 24, 2024Abstract:Neural operators such as the Fourier Neural Operator (FNO) have been shown to provide resolution-independent deep learning models that can learn mappings between function spaces. For example, an initial condition can be mapped to the solution of a partial differential equation (PDE) at a future time-step using a neural operator. Despite the popularity of neural operators, their use to predict solution functions over a domain given only data over the boundary (such as a spatially varying Dirichlet boundary condition) remains unexplored. In this paper, we refer to such problems as boundary-to-domain problems; they have a wide range of applications in areas such as fluid mechanics, solid mechanics, heat transfer etc. We present a novel FNO-based architecture, named Lifting Product FNO (or LP-FNO) which can map arbitrary boundary functions defined on the lower-dimensional boundary to a solution in the entire domain. Specifically, two FNOs defined on the lower-dimensional boundary are lifted into the higher dimensional domain using our proposed lifting product layer. We demonstrate the efficacy and resolution independence of the proposed LP-FNO for the 2D Poisson equation.
Scalable Artificial Intelligence for Science: Perspectives, Methods and Exemplars
Jun 24, 2024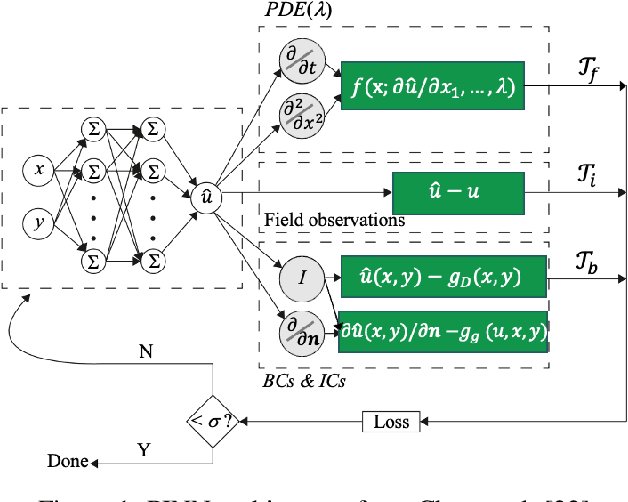
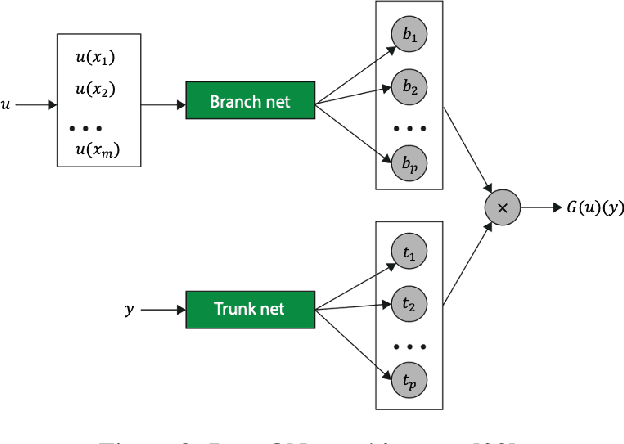
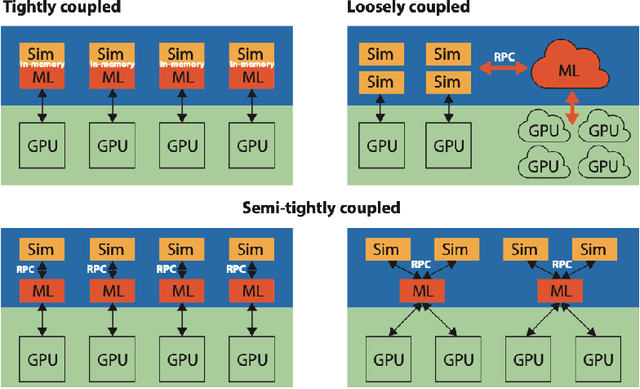
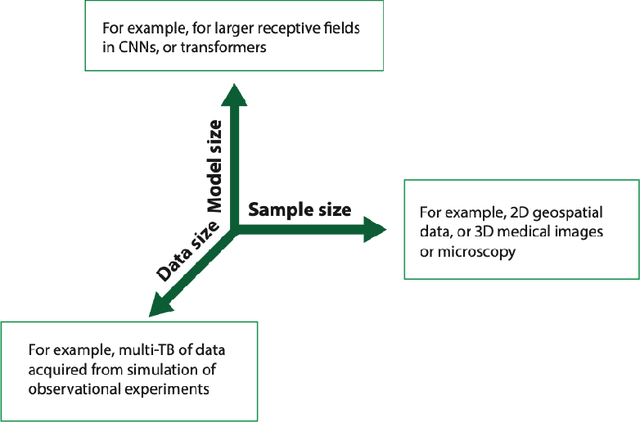
Abstract:In a post-ChatGPT world, this paper explores the potential of leveraging scalable artificial intelligence for scientific discovery. We propose that scaling up artificial intelligence on high-performance computing platforms is essential to address such complex problems. This perspective focuses on scientific use cases like cognitive simulations, large language models for scientific inquiry, medical image analysis, and physics-informed approaches. The study outlines the methodologies needed to address such challenges at scale on supercomputers or the cloud and provides exemplars of such approaches applied to solve a variety of scientific problems.
Machine-Learned Closure of URANS for Stably Stratified Turbulence: Connecting Physical Timescales & Data Hyperparameters of Deep Time-Series Models
Apr 24, 2024



Abstract:We develop time-series machine learning (ML) methods for closure modeling of the Unsteady Reynolds Averaged Navier Stokes (URANS) equations applied to stably stratified turbulence (SST). SST is strongly affected by fine balances between forces and becomes more anisotropic in time for decaying cases. Moreover, there is a limited understanding of the physical phenomena described by some of the terms in the URANS equations. Rather than attempting to model each term separately, it is attractive to explore the capability of machine learning to model groups of terms, i.e., to directly model the force balances. We consider decaying SST which are homogeneous and stably stratified by a uniform density gradient, enabling dimensionality reduction. We consider two time-series ML models: Long Short-Term Memory (LSTM) and Neural Ordinary Differential Equation (NODE). Both models perform accurately and are numerically stable in a posteriori tests. Furthermore, we explore the data requirements of the ML models by extracting physically relevant timescales of the complex system. We find that the ratio of the timescales of the minimum information required by the ML models to accurately capture the dynamics of the SST corresponds to the Reynolds number of the flow. The current framework provides the backbone to explore the capability of such models to capture the dynamics of higher-dimensional complex SST flows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge