Adversarial Boot Camp: label free certified robustness in one epoch

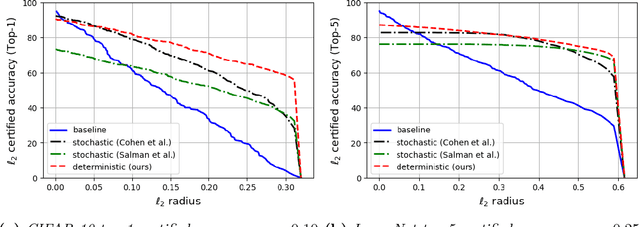
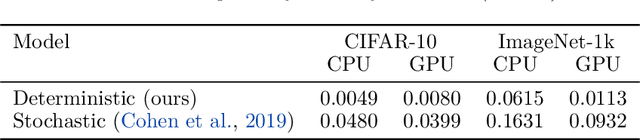
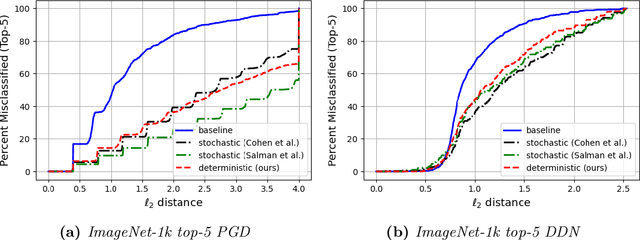
Machine learning models are vulnerable to adversarial attacks. One approach to addressing this vulnerability is certification, which focuses on models that are guaranteed to be robust for a given perturbation size. A drawback of recent certified models is that they are stochastic: they require multiple computationally expensive model evaluations with random noise added to a given input. In our work, we present a deterministic certification approach which results in a certifiably robust model. This approach is based on an equivalence between training with a particular regularized loss, and the expected values of Gaussian averages. We achieve certified models on ImageNet-1k by retraining a model with this loss for one epoch without the use of label information.

Deterministic Gaussian Averaged Neural Networks

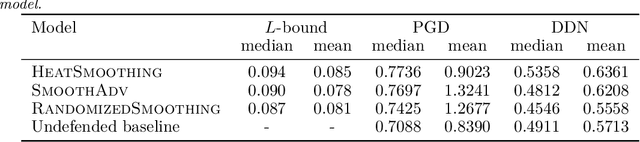
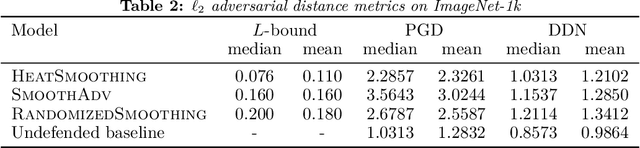
We present a deterministic method to compute the Gaussian average of neural networks used in regression and classification. Our method is based on an equivalence between training with a particular regularized loss, and the expected values of Gaussian averages. We use this equivalence to certify models which perform well on clean data but are not robust to adversarial perturbations. In terms of certified accuracy and adversarial robustness, our method is comparable to known stochastic methods such as randomized smoothing, but requires only a single model evaluation during inference.

Learning normalizing flows from Entropy-Kantorovich potentials

We approach the problem of learning continuous normalizing flows from a dual perspective motivated by entropy-regularized optimal transport, in which continuous normalizing flows are cast as gradients of scalar potential functions. This formulation allows us to train a dual objective comprised only of the scalar potential functions, and removes the burden of explicitly computing normalizing flows during training. After training, the normalizing flow is easily recovered from the potential functions.

How to train your neural ODE

Training neural ODEs on large datasets has not been tractable due to the necessity of allowing the adaptive numerical ODE solver to refine its step size to very small values. In practice this leads to dynamics equivalent to many hundreds or even thousands of layers. In this paper, we overcome this apparent difficulty by introducing a theoretically-grounded combination of both optimal transport and stability regularizations which encourage neural ODEs to prefer simpler dynamics out of all the dynamics that solve a problem well. Simpler dynamics lead to faster convergence and to fewer discretizations of the solver, considerably decreasing wall-clock time without loss in performance. Our approach allows us to train neural ODE based generative models to the same performance as the unregularized dynamics in just over a day on one GPU, whereas unregularized dynamics can take up to 4-6 days of training time on multiple GPUs. This brings neural ODEs significantly closer to practical relevance in large-scale applications.

Farkas layers: don't shift the data, fix the geometry

Successfully training deep neural networks often requires either batch normalization, appropriate weight initialization, both of which come with their own challenges. We propose an alternative, geometrically motivated method for training. Using elementary results from linear programming, we introduce Farkas layers: a method that ensures at least one neuron is active at a given layer. Focusing on residual networks with ReLU activation, we empirically demonstrate a significant improvement in training capacity in the absence of batch normalization or methods of initialization across a broad range of network sizes on benchmark datasets.

Partial differential equation regularization for supervised machine learning

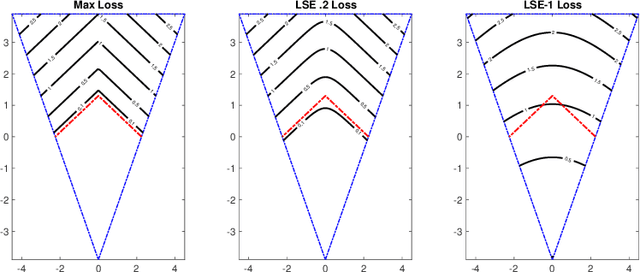
This article is an overview of supervised machine learning problems for regression and classification. Topics include: kernel methods, training by stochastic gradient descent, deep learning architecture, losses for classification, statistical learning theory, and dimension independent generalization bounds. Implicit regularization in deep learning examples are presented, including data augmentation, adversarial training, and additive noise. These methods are reframed as explicit gradient regularization.

Scaleable input gradient regularization for adversarial robustness

Input gradient regularization is not thought to be an effective means for promoting adversarial robustness. In this work we revisit this regularization scheme with some new ingredients. First, we derive new per-image theoretical robustness bounds based on local gradient information, and curvature information when available. These bounds strongly motivate input gradient regularization. Second, we implement a scaleable version of input gradient regularization which avoids double backpropagation: adversarially robust ImageNet models are trained in 33 hours on four consumer grade GPUs. Finally, we show experimentally that input gradient regularization is competitive with adversarial training.

Lipschitz regularized Deep Neural Networks converge and generalize

Generalization of deep neural networks (DNNs) is an open problem which, if solved, could impact the reliability and verification of deep neural network architectures. In this paper, we show that if the usual fidelity term used in training DNNs is augmented by a Lipschitz regularization term, then the networks converge and generalize. The convergence is in the limit as the number of data points, $n\to \infty$, while also allowing the network to grow as needed to fit the data. Two regimes are identified: in the case of clean labels, we prove convergence to the label function which corresponds to zero loss, in the case of corrupted labels which we prove convergence to a regularized label function which is the solution of a limiting variational problem. In both cases, a convergence rate is also provided.