Preference-Based Planning in Stochastic Environments: From Partially-Ordered Temporal Goals to Most Preferred Policies

Human preferences are not always represented via complete linear orders: It is natural to employ partially-ordered preferences for expressing incomparable outcomes. In this work, we consider decision-making and probabilistic planning in stochastic systems modeled as Markov decision processes (MDPs), given a partially ordered preference over a set of temporally extended goals. Specifically, each temporally extended goal is expressed using a formula in Linear Temporal Logic on Finite Traces (LTL$_f$). To plan with the partially ordered preference, we introduce order theory to map a preference over temporal goals to a preference over policies for the MDP. Accordingly, a most preferred policy under a stochastic ordering induces a stochastic nondominated probability distribution over the finite paths in the MDP. To synthesize a most preferred policy, our technical approach includes two key steps. In the first step, we develop a procedure to transform a partially ordered preference over temporal goals into a computational model, called preference automaton, which is a semi-automaton with a partial order over acceptance conditions. In the second step, we prove that finding a most preferred policy is equivalent to computing a Pareto-optimal policy in a multi-objective MDP that is constructed from the original MDP, the preference automaton, and the chosen stochastic ordering relation. Throughout the paper, we employ running examples to illustrate the proposed preference specification and solution approaches. We demonstrate the efficacy of our algorithm using these examples, providing detailed analysis, and then discuss several potential future directions.

Opportunistic Qualitative Planning in Stochastic Systems with Incomplete Preferences over Reachability Objectives

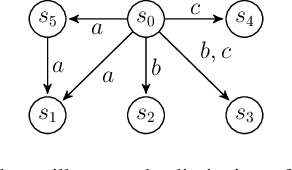
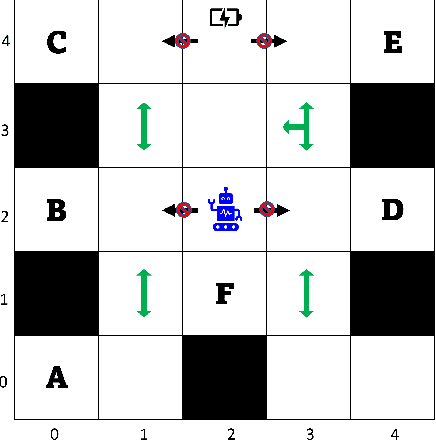
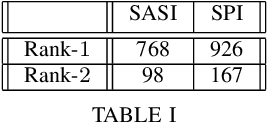
Preferences play a key role in determining what goals/constraints to satisfy when not all constraints can be satisfied simultaneously. In this paper, we study how to synthesize preference satisfying plans in stochastic systems, modeled as an MDP, given a (possibly incomplete) combinative preference model over temporally extended goals. We start by introducing new semantics to interpret preferences over infinite plays of the stochastic system. Then, we introduce a new notion of improvement to enable comparison between two prefixes of an infinite play. Based on this, we define two solution concepts called safe and positively improving (SPI) and safe and almost-surely improving (SASI) that enforce improvements with a positive probability and with probability one, respectively. We construct a model called an improvement MDP, in which the synthesis of SPI and SASI strategies that guarantee at least one improvement reduces to computing positive and almost-sure winning strategies in an MDP. We present an algorithm to synthesize the SPI and SASI strategies that induce multiple sequential improvements. We demonstrate the proposed approach using a robot motion planning problem.

Probabilistic Planning with Partially Ordered Preferences over Temporal Goals

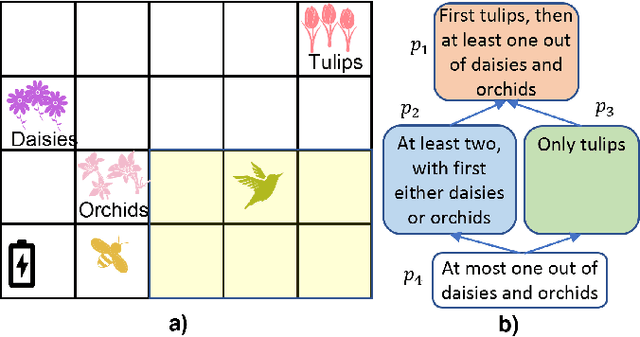
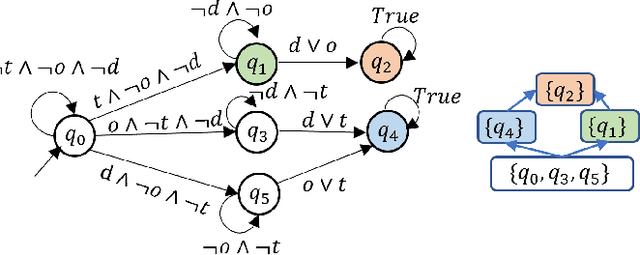
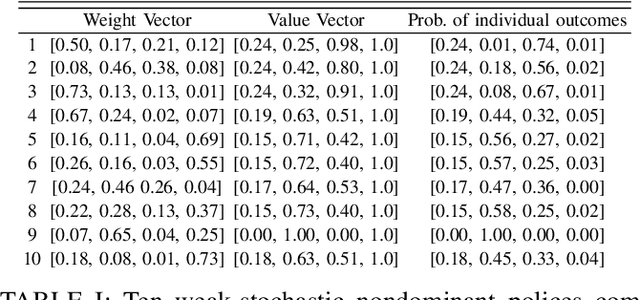
In this paper, we study planning in stochastic systems, modeled as Markov decision processes (MDPs), with preferences over temporally extended goals. Prior work on temporal planning with preferences assumes that the user preferences form a total order, meaning that every pair of outcomes are comparable with each other. In this work, we consider the case where the preferences over possible outcomes are a partial order rather than a total order. We first introduce a variant of deterministic finite automaton, referred to as a preference DFA, for specifying the user's preferences over temporally extended goals. Based on the order theory, we translate the preference DFA to a preference relation over policies for probabilistic planning in a labeled MDP. In this treatment, a most preferred policy induces a weak-stochastic nondominated probability distribution over the finite paths in the MDP. The proposed planning algorithm hinges on the construction of a multi-objective MDP. We prove that a weak-stochastic nondominated policy given the preference specification is Pareto-optimal in the constructed multi-objective MDP, and vice versa. Throughout the paper, we employ a running example to demonstrate the proposed preference specification and solution approaches. We show the efficacy of our algorithm using the example with detailed analysis, and then discuss possible future directions.

A Theory of Hypergames on Graphs for Synthesizing Dynamic Cyber Defense with Deception

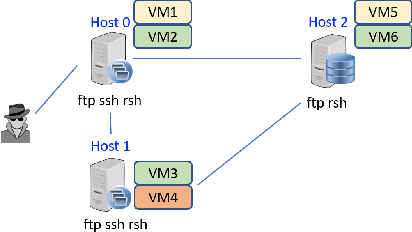
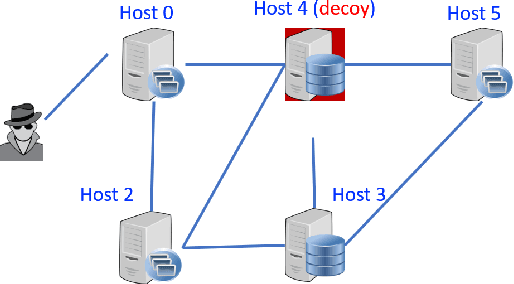
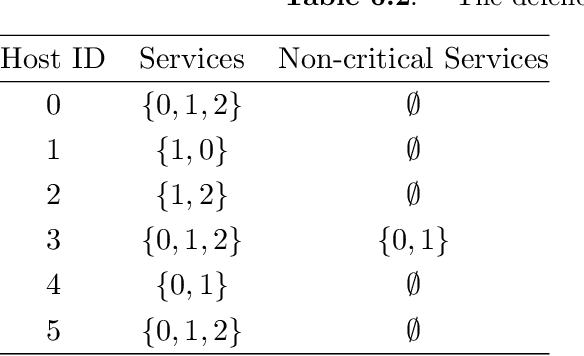
In this chapter, we present an approach using formal methods to synthesize reactive defense strategy in a cyber network, equipped with a set of decoy systems. We first generalize formal graphical security models--attack graphs--to incorporate defender's countermeasures in a game-theoretic model, called an attack-defend game on graph. This game captures the dynamic interactions between the defender and the attacker and their defense/attack objectives in formal logic. Then, we introduce a class of hypergames to model asymmetric information created by decoys in the attacker-defender interactions. Given qualitative security specifications in formal logic, we show that the solution concepts from hypergames and reactive synthesis in formal methods can be extended to synthesize effective dynamic defense strategy using cyber deception. The strategy takes the advantages of the misperception of the attacker to ensure security specification is satisfied, which may not be satisfiable when the information is symmetric.