Hazhar Rahmani
Automata Learning of Preferences over Temporal Logic Formulas from Pairwise Comparisons
May 23, 2025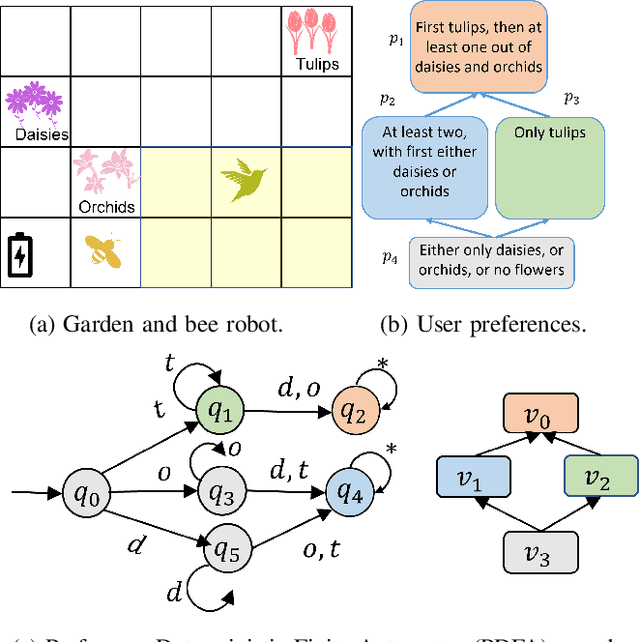

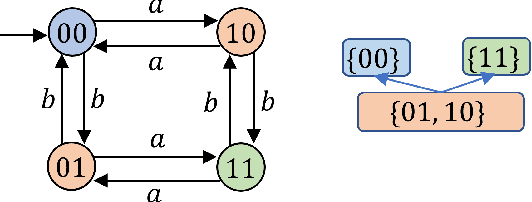
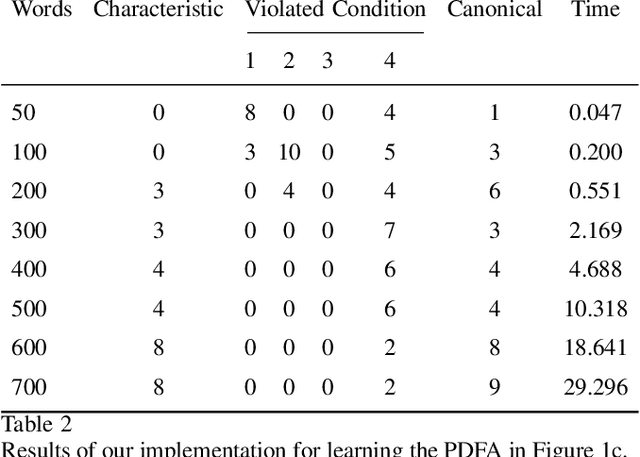
Abstract:Many preference elicitation algorithms consider preference over propositional logic formulas or items with different attributes. In sequential decision making, a user's preference can be a preorder over possible outcomes, each of which is a temporal sequence of events. This paper considers a class of preference inference problems where the user's unknown preference is represented by a preorder over regular languages (sets of temporal sequences), referred to as temporal goals. Given a finite set of pairwise comparisons between finite words, the objective is to learn both the set of temporal goals and the preorder over these goals. We first show that a preference relation over temporal goals can be modeled by a Preference Deterministic Finite Automaton (PDFA), which is a deterministic finite automaton augmented with a preorder over acceptance conditions. The problem of preference inference reduces to learning the PDFA. This problem is shown to be computationally challenging, with the problem of determining whether there exists a PDFA of size smaller than a given integer $k$, consistent with the sample, being NP-Complete. We formalize the properties of characteristic samples and develop an algorithm that guarantees to learn, given a characteristic sample, the minimal PDFA equivalent to the true PDFA from which the sample is drawn. We present the method through a running example and provide detailed analysis using a robotic motion planning problem.
Optimal sensor deception in stochastic environments with partial observability to mislead a robot to a decoy goal
Mar 07, 2025Abstract:Deception is a common strategy adapted by autonomous systems in adversarial settings. Existing deception methods primarily focus on increasing opacity or misdirecting agents away from their goal or itinerary. In this work, we propose a deception problem aiming to mislead the robot towards a decoy goal through altering sensor events under a constrained budget of alteration. The environment along with the robot's interaction with it is modeled as a Partially Observable Markov Decision Process (POMDP), and the robot's action selection is governed by a Finite State Controller (FSC). Given a constrained budget for sensor event modifications, the objective is to compute a sensor alteration that maximizes the probability of the robot reaching a decoy goal. We establish the computational hardness of the problem by a reduction from the $0/1$ Knapsack problem and propose a Mixed Integer Linear Programming (MILP) formulation to compute optimal deception strategies. We show the efficacy of our MILP formulation via a sequence of experiments.
Preference-Based Planning in Stochastic Environments: From Partially-Ordered Temporal Goals to Most Preferred Policies
Mar 27, 2024Abstract:Human preferences are not always represented via complete linear orders: It is natural to employ partially-ordered preferences for expressing incomparable outcomes. In this work, we consider decision-making and probabilistic planning in stochastic systems modeled as Markov decision processes (MDPs), given a partially ordered preference over a set of temporally extended goals. Specifically, each temporally extended goal is expressed using a formula in Linear Temporal Logic on Finite Traces (LTL$_f$). To plan with the partially ordered preference, we introduce order theory to map a preference over temporal goals to a preference over policies for the MDP. Accordingly, a most preferred policy under a stochastic ordering induces a stochastic nondominated probability distribution over the finite paths in the MDP. To synthesize a most preferred policy, our technical approach includes two key steps. In the first step, we develop a procedure to transform a partially ordered preference over temporal goals into a computational model, called preference automaton, which is a semi-automaton with a partial order over acceptance conditions. In the second step, we prove that finding a most preferred policy is equivalent to computing a Pareto-optimal policy in a multi-objective MDP that is constructed from the original MDP, the preference automaton, and the chosen stochastic ordering relation. Throughout the paper, we employ running examples to illustrate the proposed preference specification and solution approaches. We demonstrate the efficacy of our algorithm using these examples, providing detailed analysis, and then discuss several potential future directions.
Optimal Sensor Deception to Deviate from an Allowed Itinerary
Aug 02, 2023



Abstract:In this work, we study a class of deception planning problems in which an agent aims to alter a security monitoring system's sensor readings so as to disguise its adversarial itinerary as an allowed itinerary in the environment. The adversarial itinerary set and allowed itinerary set are captured by regular languages. To deviate without being detected, we investigate whether there exists a strategy for the agent to alter the sensor readings, with a minimal cost, such that for any of those paths it takes, the system thinks the agent took a path within the allowed itinerary. Our formulation assumes an offline sensor alteration where the agent determines the sensor alteration strategy and implement it, and then carry out any path in its deviation itinerary. We prove that the problem of solving the optimal sensor alteration is NP-hard, by a reduction from the directed multi-cut problem. Further, we present an exact algorithm based on integer linear programming and demonstrate the correctness and the efficacy of the algorithm in case studies.
Probabilistic Planning with Prioritized Preferences over Temporal Logic Objectives
Apr 23, 2023Abstract:This paper studies temporal planning in probabilistic environments, modeled as labeled Markov decision processes (MDPs), with user preferences over multiple temporal goals. Existing works reflect such preferences as a prioritized list of goals. This paper introduces a new specification language, termed prioritized qualitative choice linear temporal logic on finite traces, which augments linear temporal logic on finite traces with prioritized conjunction and ordered disjunction from prioritized qualitative choice logic. This language allows for succinctly specifying temporal objectives with corresponding preferences accomplishing each temporal task. The finite traces that describe the system's behaviors are ranked based on their dissatisfaction scores with respect to the formula. We propose a systematic translation from the new language to a weighted deterministic finite automaton. Utilizing this computational model, we formulate and solve a problem of computing an optimal policy that minimizes the expected score of dissatisfaction given user preferences. We demonstrate the efficacy and applicability of the logic and the algorithm on several case studies with detailed analyses for each.
Probabilistic Planning with Partially Ordered Preferences over Temporal Goals
Sep 25, 2022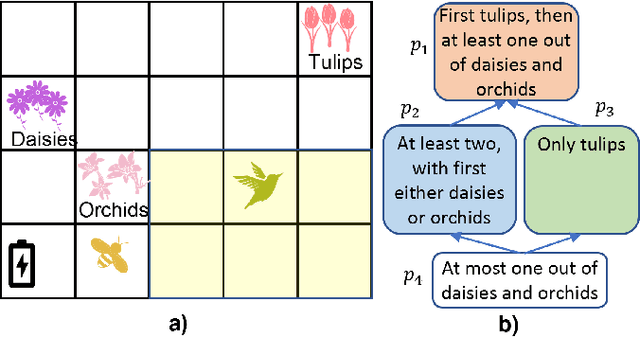
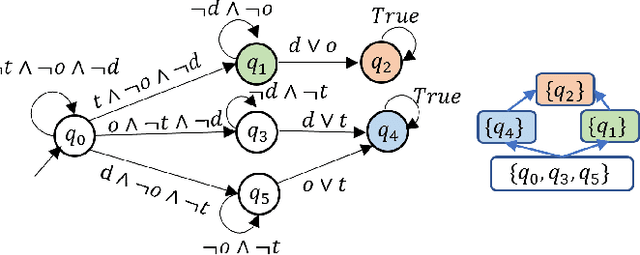
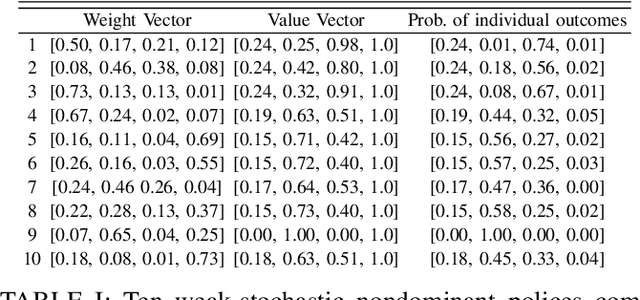
Abstract:In this paper, we study planning in stochastic systems, modeled as Markov decision processes (MDPs), with preferences over temporally extended goals. Prior work on temporal planning with preferences assumes that the user preferences form a total order, meaning that every pair of outcomes are comparable with each other. In this work, we consider the case where the preferences over possible outcomes are a partial order rather than a total order. We first introduce a variant of deterministic finite automaton, referred to as a preference DFA, for specifying the user's preferences over temporally extended goals. Based on the order theory, we translate the preference DFA to a preference relation over policies for probabilistic planning in a labeled MDP. In this treatment, a most preferred policy induces a weak-stochastic nondominated probability distribution over the finite paths in the MDP. The proposed planning algorithm hinges on the construction of a multi-objective MDP. We prove that a weak-stochastic nondominated policy given the preference specification is Pareto-optimal in the constructed multi-objective MDP, and vice versa. Throughout the paper, we employ a running example to demonstrate the proposed preference specification and solution approaches. We show the efficacy of our algorithm using the example with detailed analysis, and then discuss possible future directions.
Sensor selection for detecting deviations from a planned itinerary
Mar 12, 2021

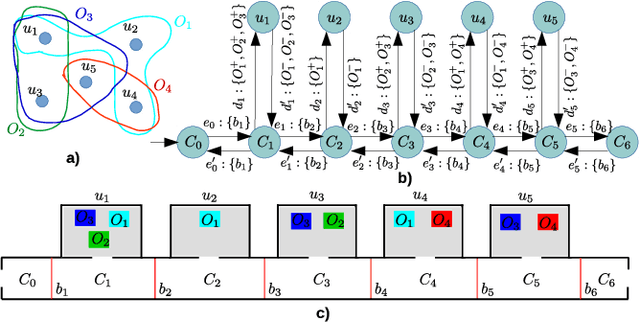
Abstract:Suppose an agent asserts that it will move through an environment in some way. When the agent executes its motion, how does one verify the claim? The problem arises in a range of contexts including in validating safety claims about robot behavior, applications in security and surveillance, and for both the conception and the (physical) design and logistics of scientific experiments. Given a set of feasible sensors to select from, we ask how to choose sensors optimally in order to ensure that the agent's execution does indeed fit its pre-disclosed itinerary. Our treatment is distinguished from prior work in sensor selection by two aspects: the form the itinerary takes (a regular language of transitions) and that families of sensor choices can be grouped as a single choice. Both are intimately tied together, permitting construction of a product automaton because the same physical sensors (i.e., the same choice) can appear multiple times. This paper establishes the hardness of sensor selection for itinerary validation within this treatment, and proposes an exact algorithm based on an ILP formulation that is capable of solving problem instances of moderate size. We demonstrate its efficacy on small-scale case studies, including one motivated by wildlife tracking.
Accelerating combinatorial filter reduction through constraints
Nov 06, 2020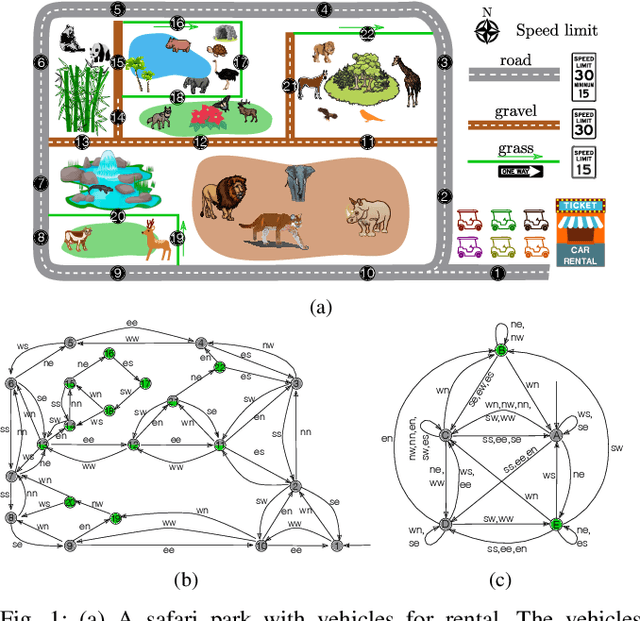
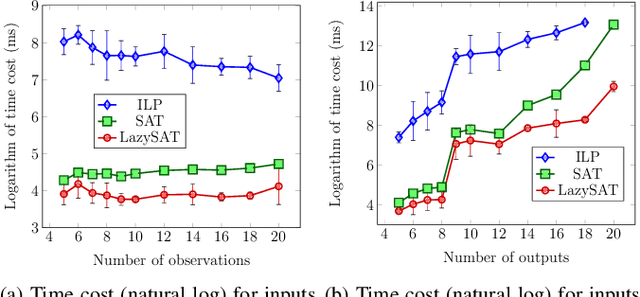
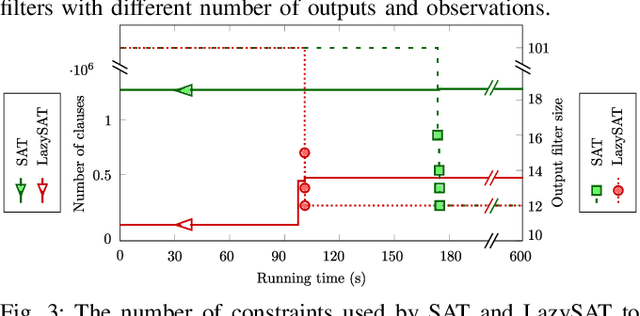
Abstract:Reduction of combinatorial filters involves compressing state representations that robots use. Such optimization arises in automating the construction of minimalist robots. But exact combinatorial filter reduction is an NP-complete problem and all current techniques are either inexact or formalized with exponentially many constraints. This paper proposes a new formalization needing only a polynomial number of constraints, and characterizes these constraints in three different forms: nonlinear, linear, and conjunctive normal form. Empirical results show that constraints in conjunctive normal form capture the problem most effectively, leading to a method that outperforms the others. Further examination indicates that a substantial proportion of constraints remain inactive during iterative filter reduction. To leverage this observation, we introduce just-in-time generation of such constraints, which yields improvements in efficiency and has the potential to minimize large filters.
Planning to Chronicle
Nov 04, 2020
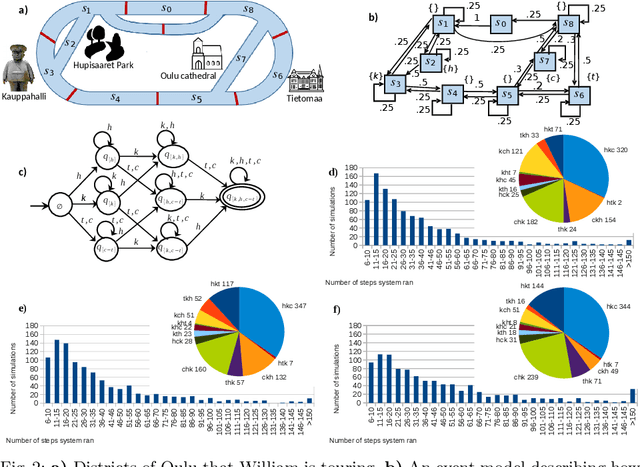
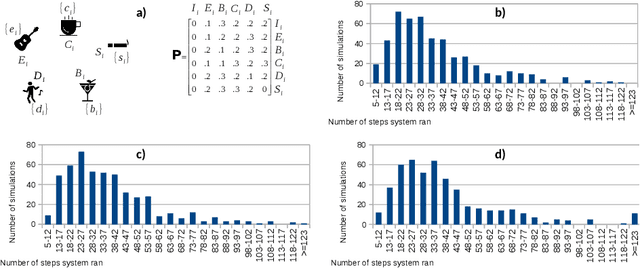
Abstract:An important class of applications entails a robot monitoring, scrutinizing, or recording the evolution of an uncertain time-extended process. This sort of situation leads an interesting family of planning problems in which the robot is limited in what it sees and must, thus, choose what to pay attention to. The distinguishing characteristic of this setting is that the robot has influence over what it captures via its sensors, but exercises no causal authority over the evolving process. As such, the robot's objective is to observe the underlying process and to produce a `chronicle' of occurrent events, subject to a goal specification of the sorts of event sequences that may be of interest. This paper examines variants of such problems when the robot aims to collect sets of observations to meet a rich specification of their sequential structure. We study this class of problems by modeling a stochastic process via a variant of a hidden Markov model, and specify the event sequences of interest as a regular language, developing a vocabulary of `mutators' that enable sophisticated requirements to be expressed. Under different suppositions about the information gleaned about the Markov model, we formulate and solve different planning problems. The core underlying idea is the construction of a product between the event model and a specification automaton. The paper reports and compares performance metrics by drawing on some small case studies analyzed in depth in simulation.
What to Do When You Can't Do It All: Temporal Logic Planning with Soft Temporal Logic Constraints
Aug 05, 2020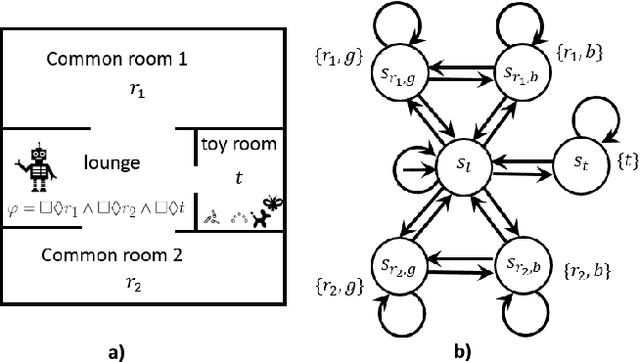


Abstract:In this paper, we consider a temporal logic planning problem in which the objective is to find an infinite trajectory that satisfies an optimal selection from a set of soft specifications expressed in linear temporal logic (LTL) while nevertheless satisfying a hard specification expressed in LTL. Our previous work considered a similar problem in which linear dynamic logic for finite traces (LDLf), rather than LTL, was used to express the soft constraints. In that work, LDLf was used to impose constraints on finite prefixes of the infinite trajectory. By using LTL, one is able not only to impose constraints on the finite prefixes of the trajectory, but also to set `soft' goals across the entirety of the infinite trajectory. Our algorithm first constructs a product automaton, on which the planning problem is reduced to computing a lasso with minimum cost. Among all such lassos, it is desirable to compute a shortest one. Though we prove that computing such a shortest lasso is computationally hard, we also introduce an efficient greedy approach to synthesize short lassos nonetheless. We present two case studies describing an implementation of this approach, and report results of our experiment comparing our greedy algorithm with an optimal baseline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge