Opportunistic Qualitative Planning in Stochastic Systems with Incomplete Preferences over Reachability Objectives
Paper and Code
Oct 04, 2022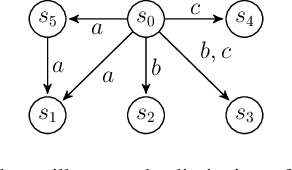
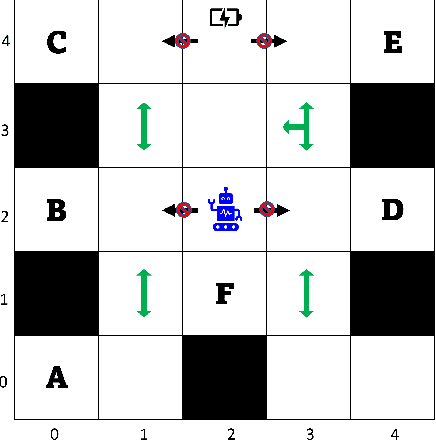
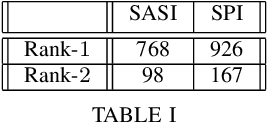
Preferences play a key role in determining what goals/constraints to satisfy when not all constraints can be satisfied simultaneously. In this paper, we study how to synthesize preference satisfying plans in stochastic systems, modeled as an MDP, given a (possibly incomplete) combinative preference model over temporally extended goals. We start by introducing new semantics to interpret preferences over infinite plays of the stochastic system. Then, we introduce a new notion of improvement to enable comparison between two prefixes of an infinite play. Based on this, we define two solution concepts called safe and positively improving (SPI) and safe and almost-surely improving (SASI) that enforce improvements with a positive probability and with probability one, respectively. We construct a model called an improvement MDP, in which the synthesis of SPI and SASI strategies that guarantee at least one improvement reduces to computing positive and almost-sure winning strategies in an MDP. We present an algorithm to synthesize the SPI and SASI strategies that induce multiple sequential improvements. We demonstrate the proposed approach using a robot motion planning problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge