Tight Mutual Information Estimation With Contrastive Fenchel-Legendre Optimization
Paper and Code
Jul 02, 2021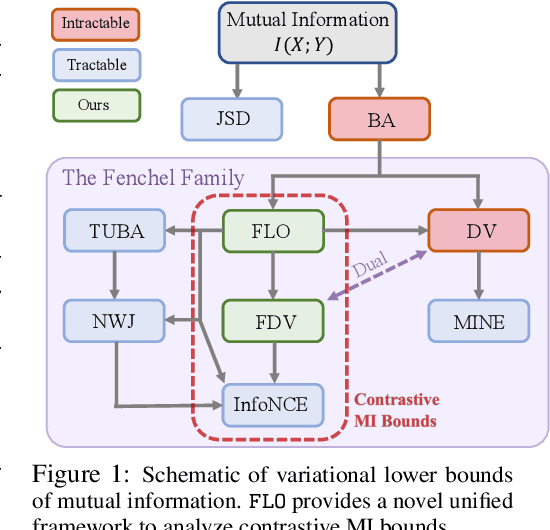
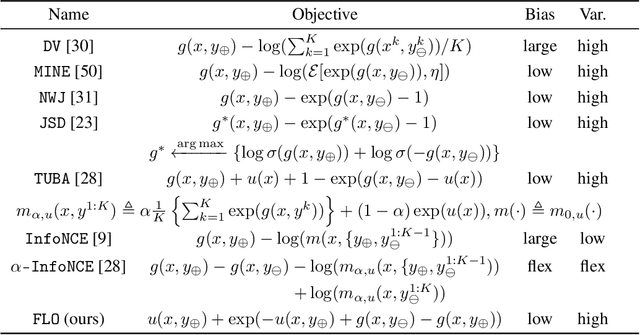
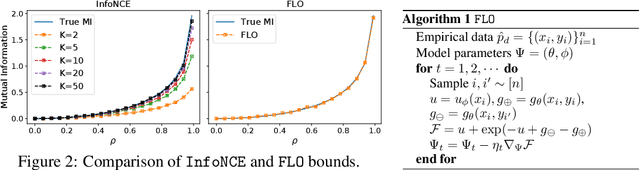

Successful applications of InfoNCE and its variants have popularized the use of contrastive variational mutual information (MI) estimators in machine learning. While featuring superior stability, these estimators crucially depend on costly large-batch training, and they sacrifice bound tightness for variance reduction. To overcome these limitations, we revisit the mathematics of popular variational MI bounds from the lens of unnormalized statistical modeling and convex optimization. Our investigation not only yields a new unified theoretical framework encompassing popular variational MI bounds but also leads to a novel, simple, and powerful contrastive MI estimator named as FLO. Theoretically, we show that the FLO estimator is tight, and it provably converges under stochastic gradient descent. Empirically, our FLO estimator overcomes the limitations of its predecessors and learns more efficiently. The utility of FLO is verified using an extensive set of benchmarks, which also reveals the trade-offs in practical MI estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge