Selectivity Estimation with Deep Likelihood Models
Paper and Code
May 10, 2019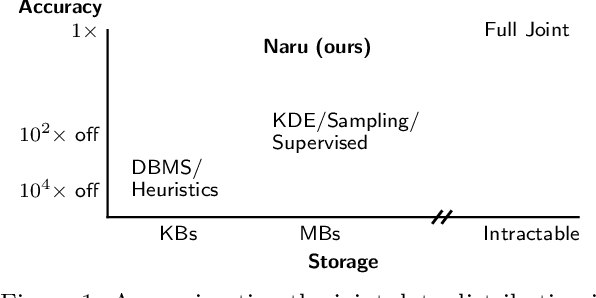
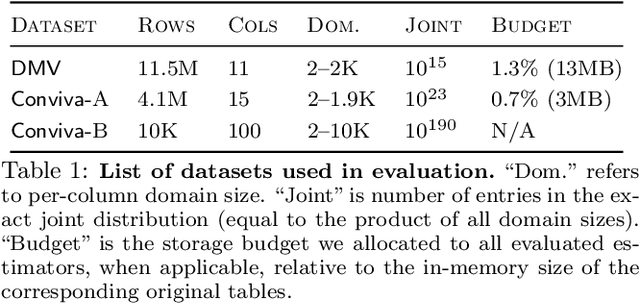
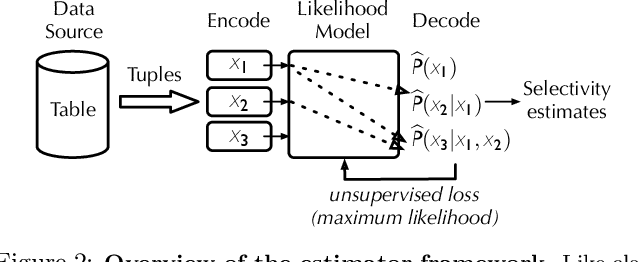
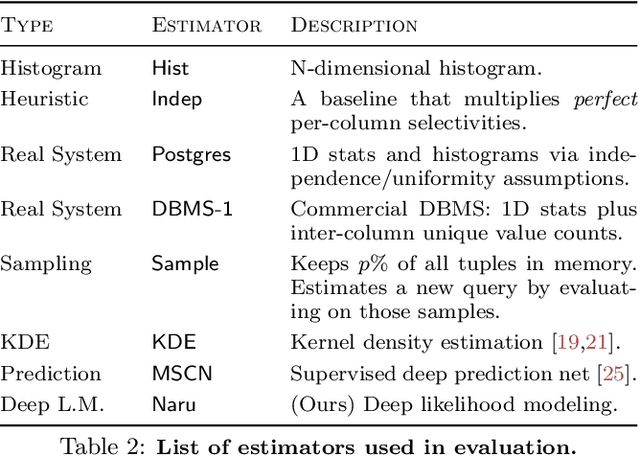
Selectivity estimation has long been grounded in statistical tools for density estimation. To capture the rich multivariate distributions of relational tables, we propose the use of a new type of high-capacity statistical model: deep likelihood models. However, direct application of these models leads to a limited estimator that is prohibitively expensive to evaluate for range and wildcard predicates. To make a truly usable estimator, we develop a Monte Carlo integration scheme on top of likelihood models that can efficiently handle range queries with dozens of filters or more. Like classical synopses, our estimator summarizes the data without supervision. Unlike previous solutions, our estimator approximates the joint data distribution without any independence assumptions. When evaluated on real-world datasets and compared against real systems and dominant families of techniques, our likelihood model based estimator achieves single-digit multiplicative error at tail, a 40-200$\times$ accuracy improvement over the second best method, and is space- and runtime-efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge