Scalable Networked Feature Selection with Randomized Algorithm for Robot Navigation

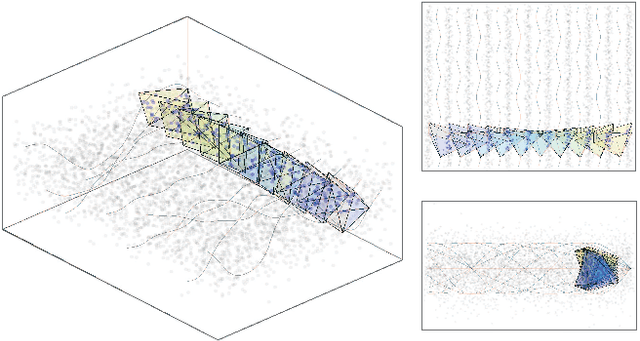
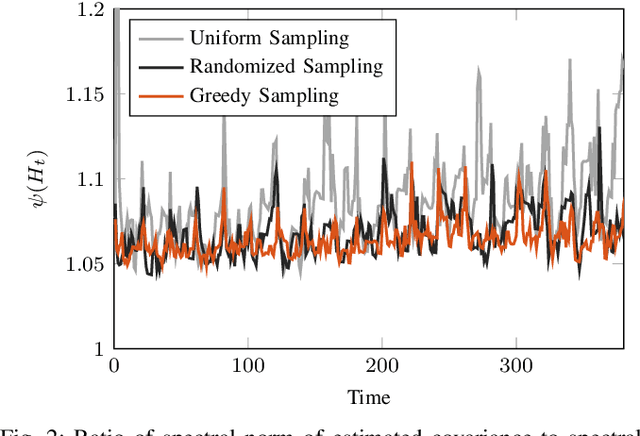
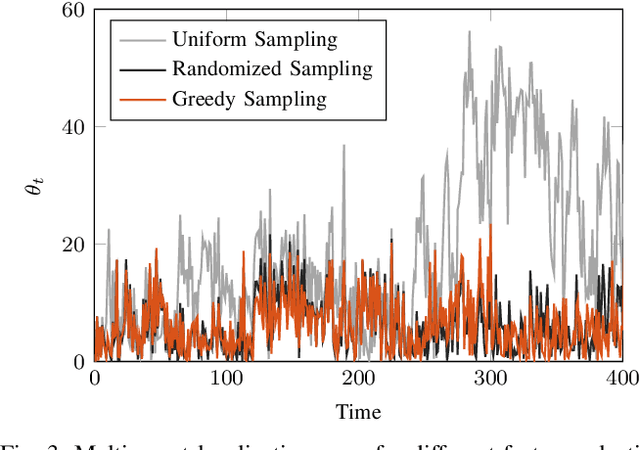
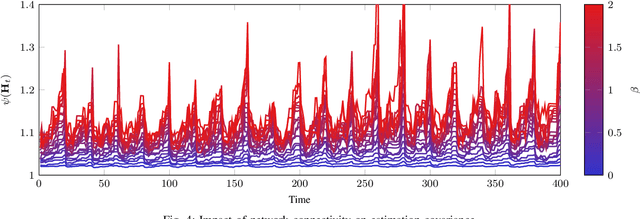
We address the problem of sparse selection of visual features for localizing a team of robots navigating an unknown environment, where robots can exchange relative position measurements with neighbors. We select a set of the most informative features by anticipating their importance in robots localization by simulating trajectories of robots over a prediction horizon. Through theoretical proofs, we establish a crucial connection between graph Laplacian and the importance of features. We show that strong network connectivity translates to uniformity in feature importance, which enables uniform random sampling of features and reduces the overall computational complexity. We leverage a scalable randomized algorithm for sparse sums of positive semidefinite matrices to efficiently select the set of the most informative features and significantly improve the probabilistic performance bounds. Finally, we support our findings with extensive simulations.