Regularization Penalty Optimization for Addressing Data Quality Variance in OoD Algorithms
Paper and Code
Jun 12, 2022
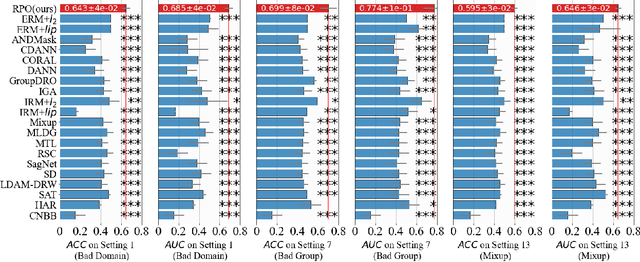

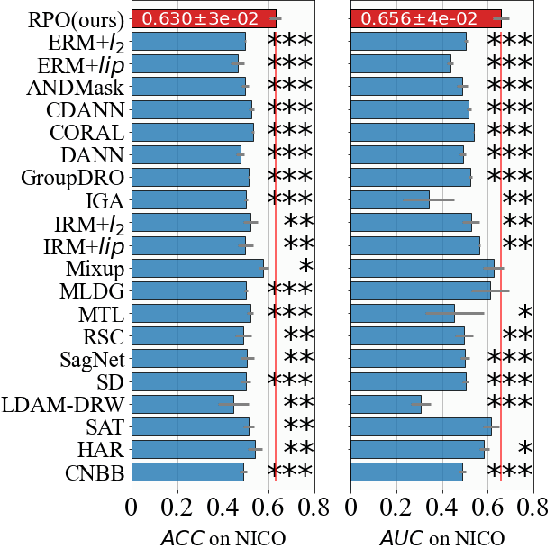
Due to the poor generalization performance of traditional empirical risk minimization (ERM) in the case of distributional shift, Out-of-Distribution (OoD) generalization algorithms receive increasing attention. However, OoD generalization algorithms overlook the great variance in the quality of training data, which significantly compromises the accuracy of these methods. In this paper, we theoretically reveal the relationship between training data quality and algorithm performance and analyze the optimal regularization scheme for Lipschitz regularized invariant risk minimization. A novel algorithm is proposed based on the theoretical results to alleviate the influence of low-quality data at both the sample level and the domain level. The experiments on both the regression and classification benchmarks validate the effectiveness of our method with statistical significance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge