OrthoReg: Improving Graph-regularized MLPs via Orthogonality Regularization
Paper and Code
Jan 31, 2023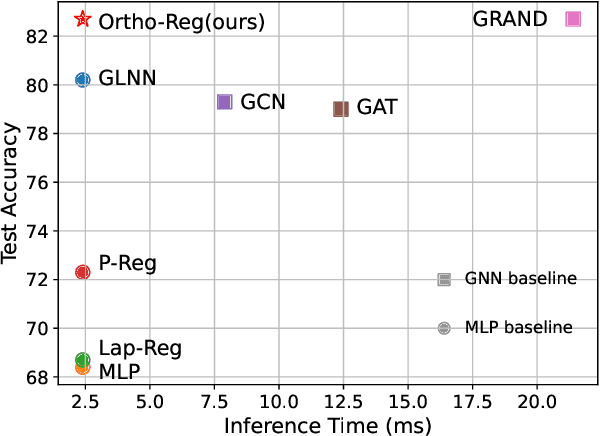
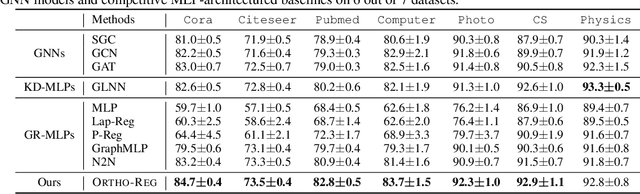
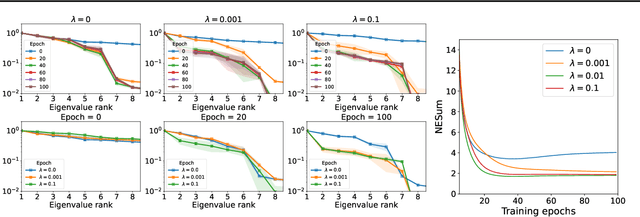
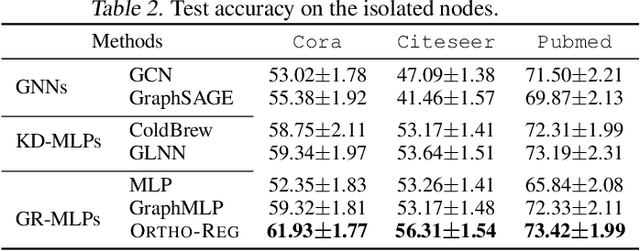
Graph Neural Networks (GNNs) are currently dominating in modeling graph-structure data, while their high reliance on graph structure for inference significantly impedes them from widespread applications. By contrast, Graph-regularized MLPs (GR-MLPs) implicitly inject the graph structure information into model weights, while their performance can hardly match that of GNNs in most tasks. This motivates us to study the causes of the limited performance of GR-MLPs. In this paper, we first demonstrate that node embeddings learned from conventional GR-MLPs suffer from dimensional collapse, a phenomenon in which the largest a few eigenvalues dominate the embedding space, through empirical observations and theoretical analysis. As a result, the expressive power of the learned node representations is constrained. We further propose OrthoReg, a novel GR-MLP model to mitigate the dimensional collapse issue. Through a soft regularization loss on the correlation matrix of node embeddings, OrthoReg explicitly encourages orthogonal node representations and thus can naturally avoid dimensionally collapsed representations. Experiments on traditional transductive semi-supervised classification tasks and inductive node classification for cold-start scenarios demonstrate its effectiveness and superiority.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge