HoMM: Higher-order Moment Matching for Unsupervised Domain Adaptation
Paper and Code
Dec 27, 2019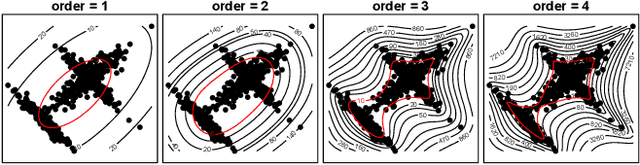
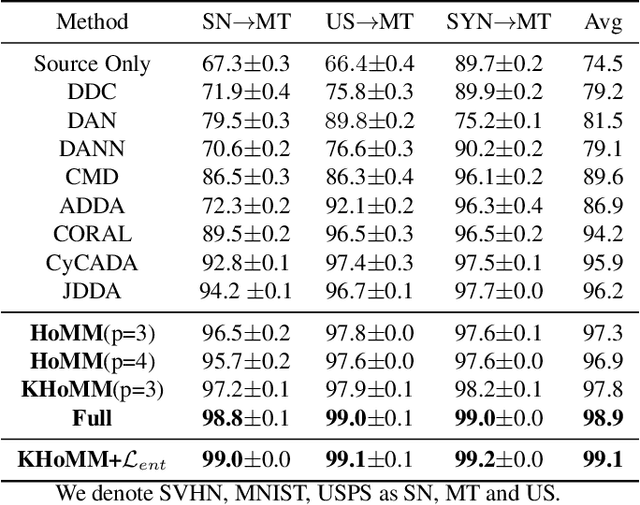
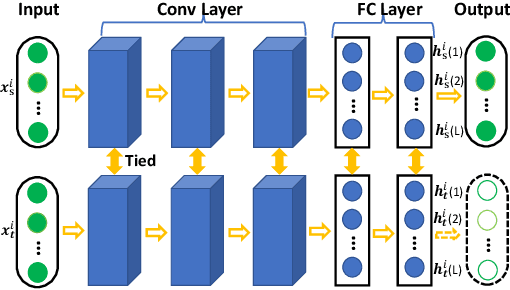
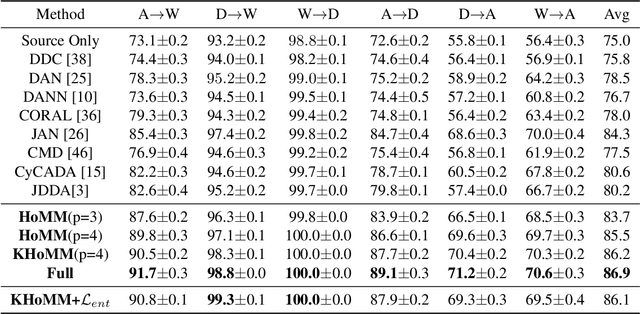
Minimizing the discrepancy of feature distributions between different domains is one of the most promising directions in unsupervised domain adaptation. From the perspective of distribution matching, most existing discrepancy-based methods are designed to match the second-order or lower statistics, which however, have limited expression of statistical characteristic for non-Gaussian distributions. In this work, we explore the benefits of using higher-order statistics (mainly refer to third-order and fourth-order statistics) for domain matching. We propose a Higher-order Moment Matching (HoMM) method, and further extend the HoMM into reproducing kernel Hilbert spaces (RKHS). In particular, our proposed HoMM can perform arbitrary-order moment tensor matching, we show that the first-order HoMM is equivalent to Maximum Mean Discrepancy (MMD) and the second-order HoMM is equivalent to Correlation Alignment (CORAL). Moreover, the third-order and the fourth-order moment tensor matching are expected to perform comprehensive domain alignment as higher-order statistics can approximate more complex, non-Gaussian distributions. Besides, we also exploit the pseudo-labeled target samples to learn discriminative representations in the target domain, which further improves the transfer performance. Extensive experiments are conducted, showing that our proposed HoMM consistently outperforms the existing moment matching methods by a large margin. Codes are available at \url{https://github.com/chenchao666/HoMM-Master}
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge