Fast and deep neuromorphic learning with time-to-first-spike coding

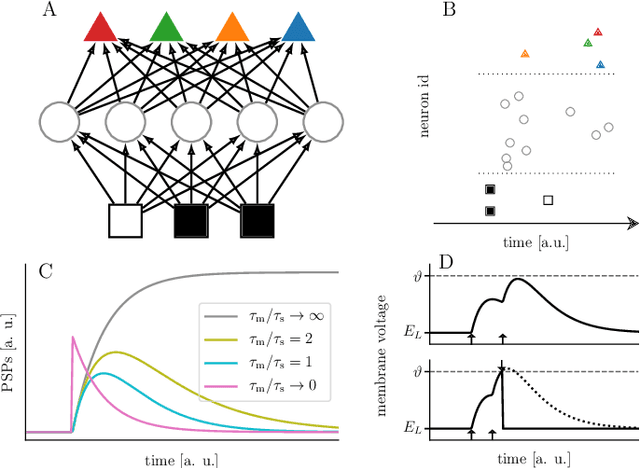
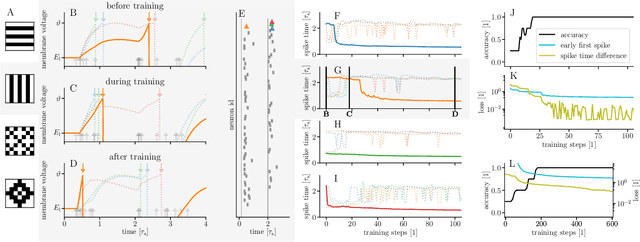
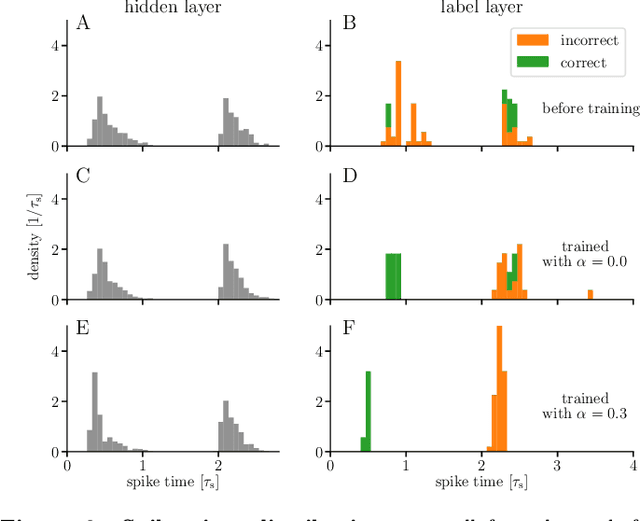
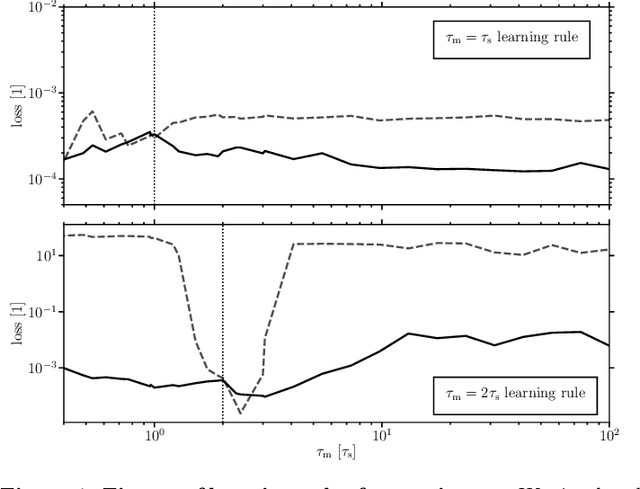
For a biological agent operating under environmental pressure, energy consumption and reaction times are of critical importance. Similarly, engineered systems also strive for short time-to-solution and low energy-to-solution characteristics. At the level of neuronal implementation, this implies achieving the desired results with as few and as early spikes as possible. In the time-to-first-spike coding framework, both of these goals are inherently emerging features of learning. Here, we describe a rigorous derivation of error-backpropagation-based learning for hierarchical networks of leaky integrate-and-fire neurons. We explicitly address two issues that are relevant for both biological plausibility and applicability to neuromorphic substrates by incorporating dynamics with finite time constants and by optimizing the backward pass with respect to substrate variability. This narrows the gap between previous models of first-spike-time learning and biological neuronal dynamics, thereby also enabling fast and energy-efficient inference on analog neuromorphic devices that inherit these dynamics from their biological archetypes, which we demonstrate on two generations of the BrainScaleS analog neuromorphic architecture.