FAM: Relative Flatness Aware Minimization
Paper and Code
Jul 05, 2023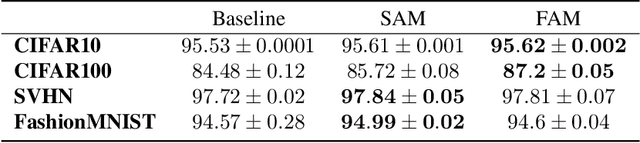
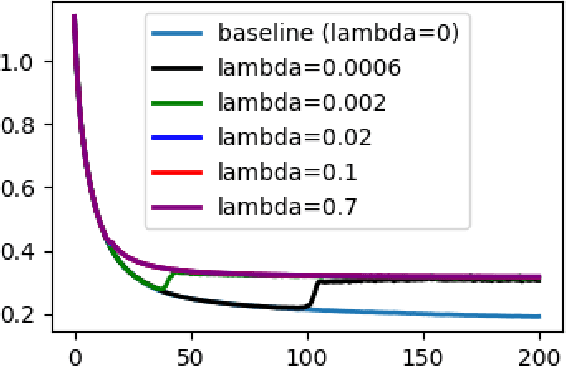
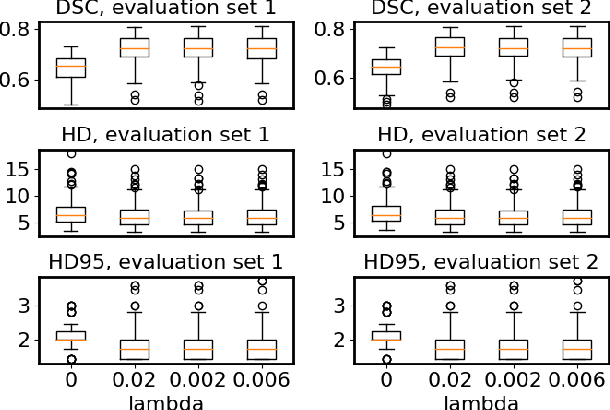

Flatness of the loss curve around a model at hand has been shown to empirically correlate with its generalization ability. Optimizing for flatness has been proposed as early as 1994 by Hochreiter and Schmidthuber, and was followed by more recent successful sharpness-aware optimization techniques. Their widespread adoption in practice, though, is dubious because of the lack of theoretically grounded connection between flatness and generalization, in particular in light of the reparameterization curse - certain reparameterizations of a neural network change most flatness measures but do not change generalization. Recent theoretical work suggests that a particular relative flatness measure can be connected to generalization and solves the reparameterization curse. In this paper, we derive a regularizer based on this relative flatness that is easy to compute, fast, efficient, and works with arbitrary loss functions. It requires computing the Hessian only of a single layer of the network, which makes it applicable to large neural networks, and with it avoids an expensive mapping of the loss surface in the vicinity of the model. In an extensive empirical evaluation we show that this relative flatness aware minimization (FAM) improves generalization in a multitude of applications and models, both in finetuning and standard training. We make the code available at github.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge