Collaborative Learning in General Graphs with Limited Memorization: Learnability, Complexity and Reliability
Paper and Code
Jan 29, 2022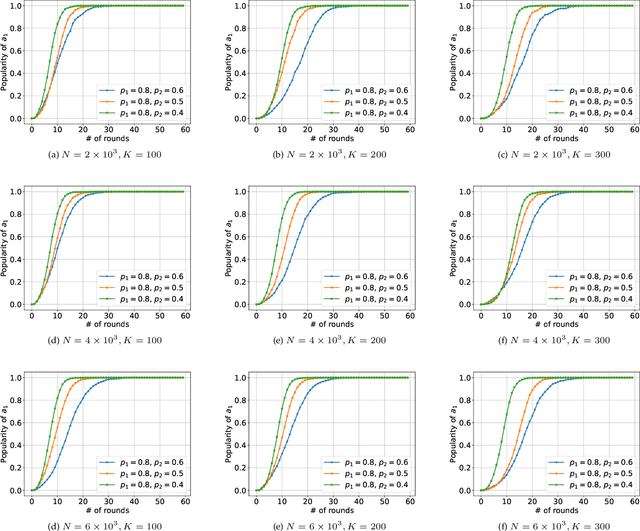
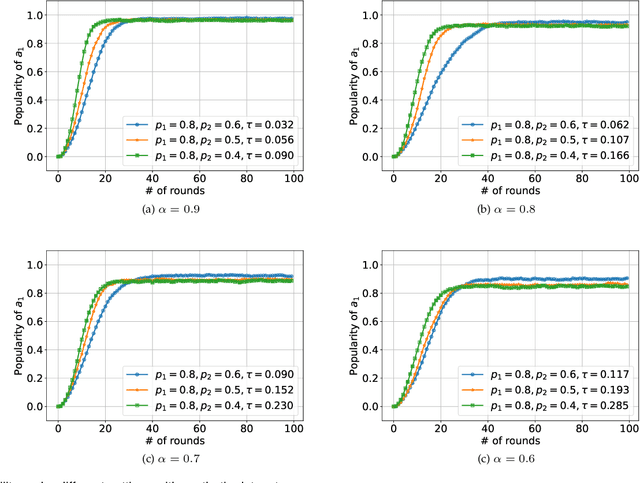
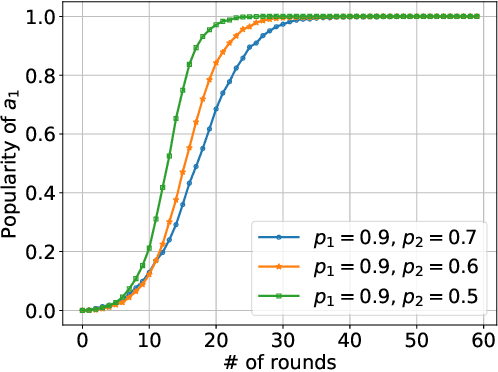
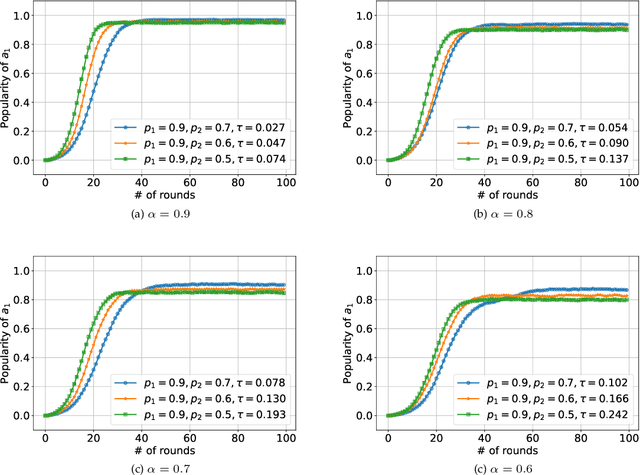
We consider K-armed bandit problem in general graphs where agents are arbitrarily connected and each of them has limited memorization and communication bandwidth. The goal is to let each of the agents learn the best arm. Although recent studies show the power of collaboration among the agents in improving the efficacy of learning, it is assumed in these studies that the communication graphs should be complete or well-structured, whereas such an assumption is not always valid in practice. Furthermore, limited memorization and communication bandwidth also restrict the collaborations of the agents, since very few knowledge can be drawn by each agent from its experiences or the ones shared by its peers in this case. Additionally, the agents may be corrupted to share falsified experience, while the resource limit may considerably restrict the reliability of the learning process. To address the above issues, we propose a three-staged collaborative learning algorithm. In each step, the agents share their experience with each other through light-weight random walks in the general graphs, and then make decisions on which arms to pull according to the randomly memorized suggestions. The agents finally update their adoptions (i.e., preferences to the arms) based on the reward feedback of the arm pulling. Our theoretical analysis shows that, by exploiting the limited memorization and communication resources, all the agents eventually learn the best arm with high probability. We also reveal in our theoretical analysis the upper-bound on the number of corrupted agents our algorithm can tolerate. The efficacy of our proposed three-staged collaborative learning algorithm is finally verified by extensive experiments on both synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge