Coagent Networks: Generalized and Scaled
Paper and Code
May 16, 2023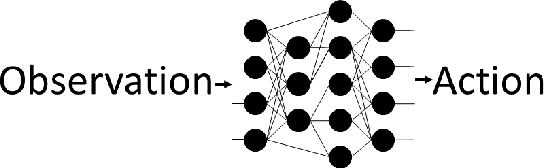

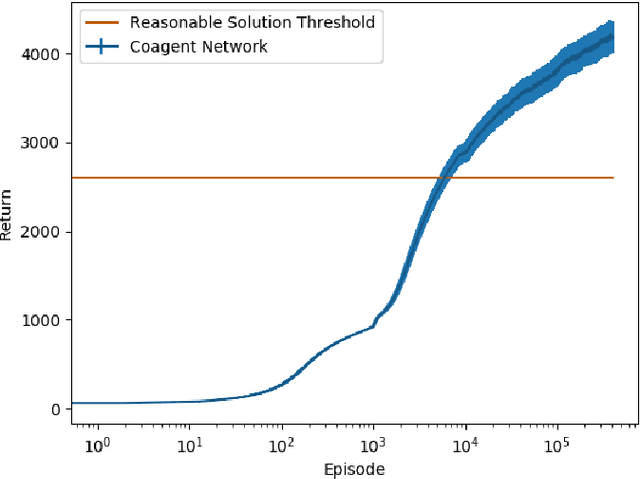
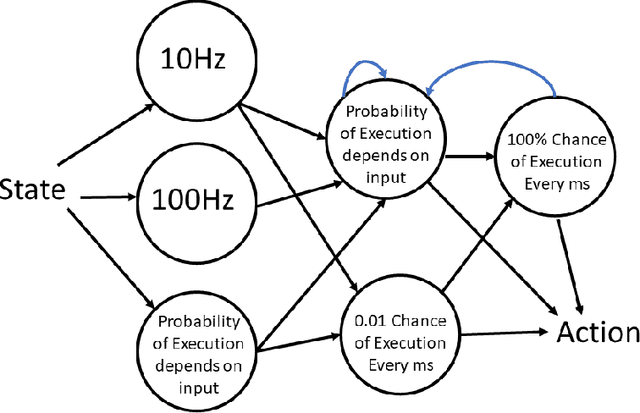
Coagent networks for reinforcement learning (RL) [Thomas and Barto, 2011] provide a powerful and flexible framework for deriving principled learning rules for arbitrary stochastic neural networks. The coagent framework offers an alternative to backpropagation-based deep learning (BDL) that overcomes some of backpropagation's main limitations. For example, coagent networks can compute different parts of the network \emph{asynchronously} (at different rates or at different times), can incorporate non-differentiable components that cannot be used with backpropagation, and can explore at levels higher than their action spaces (that is, they can be designed as hierarchical networks for exploration and/or temporal abstraction). However, the coagent framework is not just an alternative to BDL; the two approaches can be blended: BDL can be combined with coagent learning rules to create architectures with the advantages of both approaches. This work generalizes the coagent theory and learning rules provided by previous works; this generalization provides more flexibility for network architecture design within the coagent framework. This work also studies one of the chief disadvantages of coagent networks: high variance updates for networks that have many coagents and do not use backpropagation. We show that a coagent algorithm with a policy network that does not use backpropagation can scale to a challenging RL domain with a high-dimensional state and action space (the MuJoCo Ant environment), learning reasonable (although not state-of-the-art) policies. These contributions motivate and provide a more general theoretical foundation for future work that studies coagent networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge