Can a Fruit Fly Learn Word Embeddings?
Paper and Code
Jan 18, 2021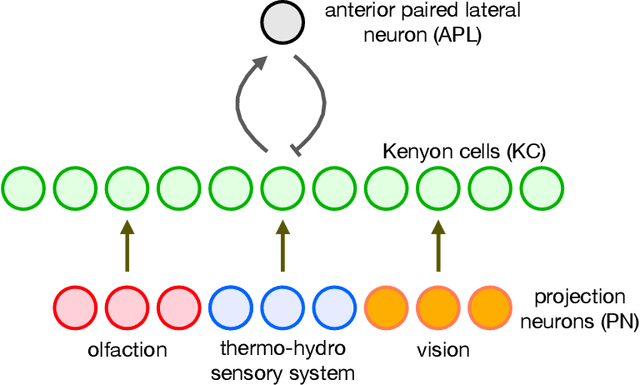
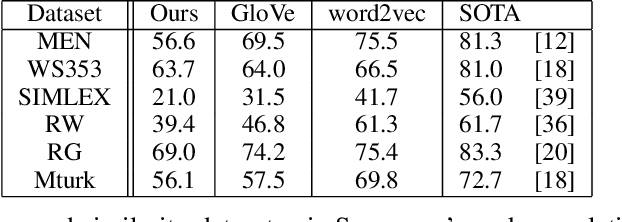
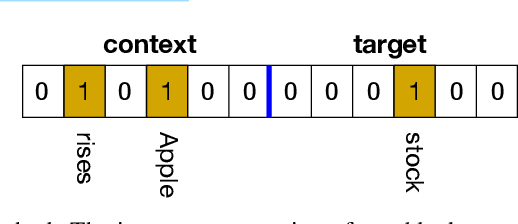

The mushroom body of the fruit fly brain is one of the best studied systems in neuroscience. At its core it consists of a population of Kenyon cells, which receive inputs from multiple sensory modalities. These cells are inhibited by the anterior paired lateral neuron, thus creating a sparse high dimensional representation of the inputs. In this work we study a mathematical formalization of this network motif and apply it to learning the correlational structure between words and their context in a corpus of unstructured text, a common natural language processing (NLP) task. We show that this network can learn semantic representations of words and can generate both static and context-dependent word embeddings. Unlike conventional methods (e.g., BERT, GloVe) that use dense representations for word embedding, our algorithm encodes semantic meaning of words and their context in the form of sparse binary hash codes. The quality of the learned representations is evaluated on word similarity analysis, word-sense disambiguation, and document classification. It is shown that not only can the fruit fly network motif achieve performance comparable to existing methods in NLP, but, additionally, it uses only a fraction of the computational resources (shorter training time and smaller memory footprint).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge