Balanced Q-learning: Combining the Influence of Optimistic and Pessimistic Targets
Paper and Code
Nov 03, 2021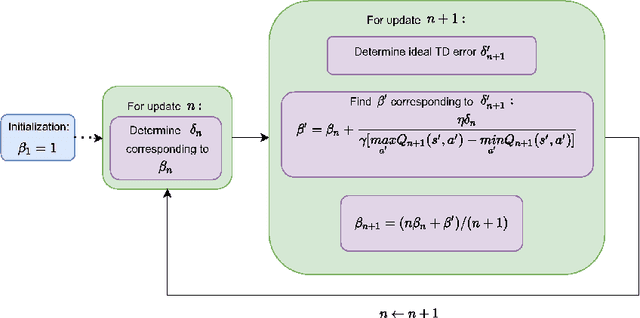
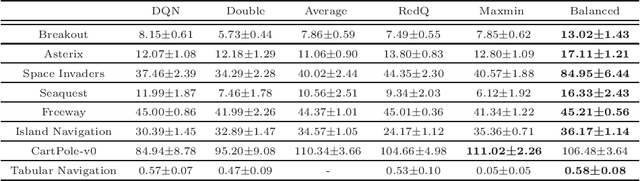
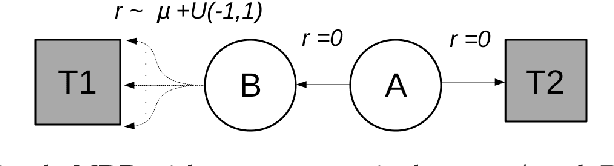
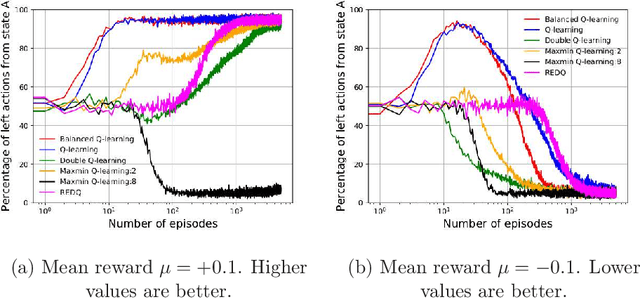
The optimistic nature of the Q-learning target leads to an overestimation bias, which is an inherent problem associated with standard $Q-$learning. Such a bias fails to account for the possibility of low returns, particularly in risky scenarios. However, the existence of biases, whether overestimation or underestimation, need not necessarily be undesirable. In this paper, we analytically examine the utility of biased learning, and show that specific types of biases may be preferable, depending on the scenario. Based on this finding, we design a novel reinforcement learning algorithm, Balanced Q-learning, in which the target is modified to be a convex combination of a pessimistic and an optimistic term, whose associated weights are determined online, analytically. We prove the convergence of this algorithm in a tabular setting, and empirically demonstrate its superior learning performance in various environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge