Semi-Aerodynamic Model Aided Invariant Kalman Filtering for UAV Full-State Estimation

Due to the state trajectory-independent features of invariant Kalman filtering (InEKF), it has attracted widespread attention in the research community for its significantly improved state estimation accuracy and convergence under disturbance. In this paper, we formulate the full-source data fusion navigation problem for fixed-wing unmanned aerial vehicle (UAV) within a framework based on error state right-invariant extended Kalman filtering (ES-RIEKF) on Lie groups. We merge measurements from a multi-rate onboard sensor network on UAVs to achieve real-time estimation of pose, air flow angles, and wind speed. Detailed derivations are provided, and the algorithm's convergence and accuracy improvements over established methods like Error State EKF (ES-EKF) and Nonlinear Complementary Filter (NCF) are demonstrated using real-flight data from UAVs. Additionally, we introduce a semi-aerodynamic model fusion framework that relies solely on ground-measurable parameters. We design and train an Long Short Term Memory (LSTM) deep network to achieve drift-free prediction of the UAV's angle of attack (AOA) and side-slip angle (SA) using easily obtainable onboard data like control surface deflections, thereby significantly reducing dependency on GNSS or complicated aerodynamic model parameters. Further, we validate the algorithm's robust advantages under GNSS denied, where flight data shows that the maximum positioning error stays within 30 meters over a 130-second denial period. To the best of our knowledge, this study is the first to apply ES-RIEKF to full-source navigation applications for fixed-wing UAVs, aiming to provide engineering references for designers. Our implementations using MATLAB/Simulink will open source.

Ziv-Zakai Bound for DOAs Estimation

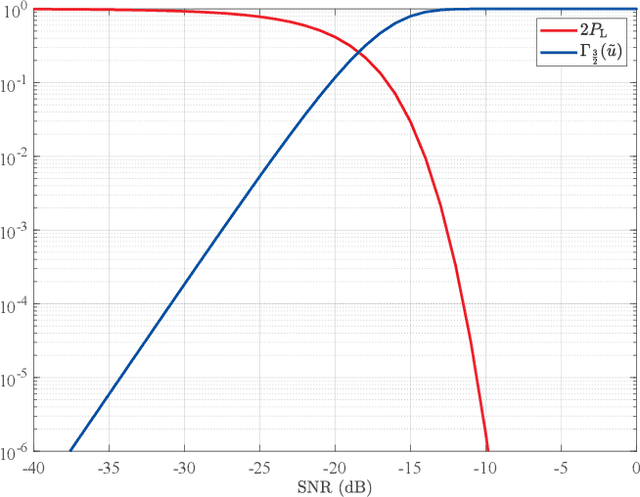
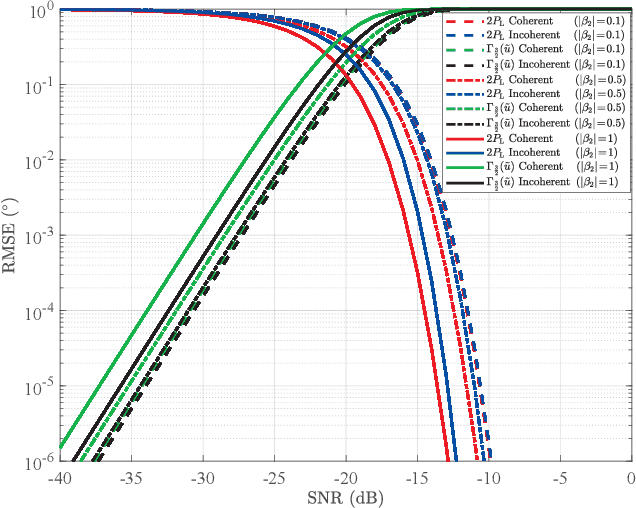
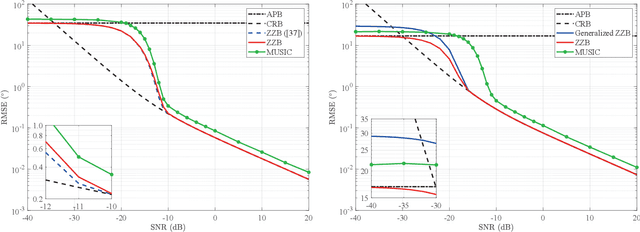
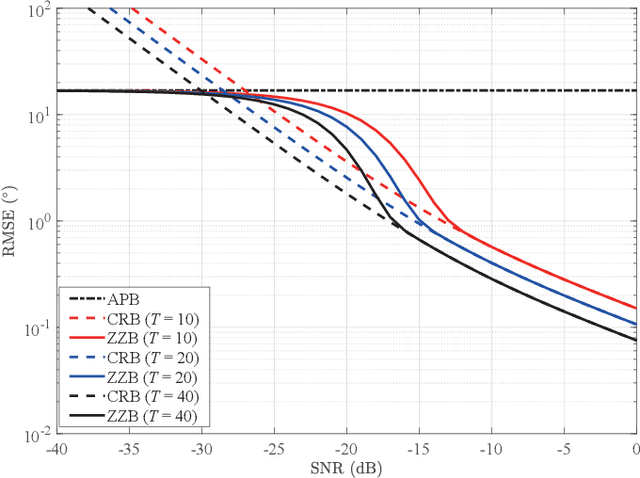
Lower bounds on the mean square error (MSE) play an important role in evaluating the estimation performance of nonlinear parameters including direction-of-arrival (DOA). Among numerous known bounds, the well-accepted Cramer-Rao bound (CRB) lower bounds the MSE in the asymptotic region only, due to its locality. By contrast, the less-adopted Ziv-Zakai bound (ZZB) is restricted by the single source assumption, although it is global tight. In this paper, we first derive an explicit ZZB applicable for hybrid coherent/incoherent multiple sources DOA estimation. In detail, we incorporate Woodbury matrix identity and Sylvester's determinant theorem to generalize the ZZB from single source DOA estimation to multiple sources DOA estimation, which, unfortunately, becomes invalid when it is far away from the asymptotic region. We then introduce the order statistics to describe the effect of ordering process during MSE calculation on the change of a priori distribution of DOAs, such that the derived ZZB can keep a tight bound on the MSE outside the asymptotic region. The derived ZZB is for the first time formulated as the function of the coherent coefficients between the coherent sources, and reveals the relationship between the MSE convergency in the a priori performance region and the number of sources. Moreover, the derived ZZB also provides a unified tight bound for both overdetermined DOAs estimation and underdetermined DOAs estimation. Simulation results demonstrate the obvious advantages of the derived ZZB over the CRB on evaluating and predicting the estimation performance of multiple sources DOA.