Ziv-Zakai Bound for DOAs Estimation

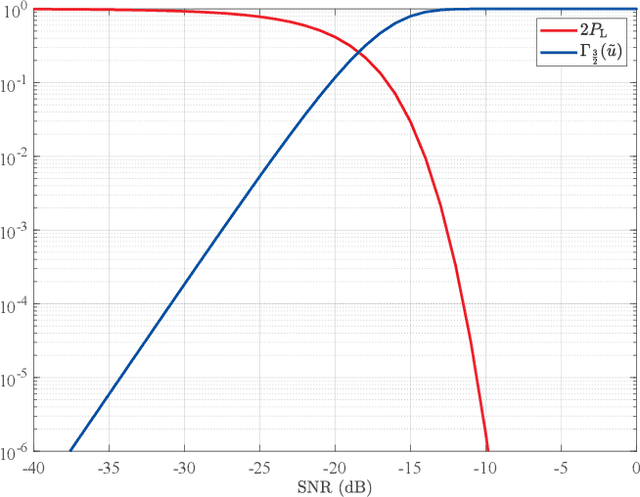
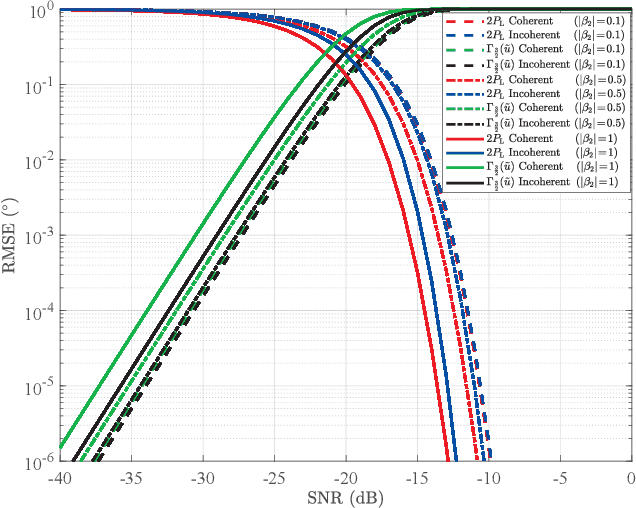
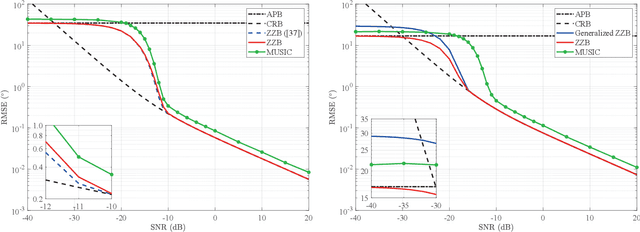
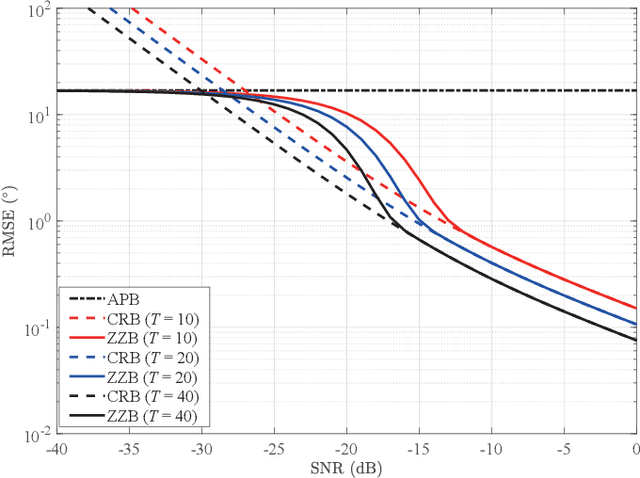
Lower bounds on the mean square error (MSE) play an important role in evaluating the estimation performance of nonlinear parameters including direction-of-arrival (DOA). Among numerous known bounds, the well-accepted Cramer-Rao bound (CRB) lower bounds the MSE in the asymptotic region only, due to its locality. By contrast, the less-adopted Ziv-Zakai bound (ZZB) is restricted by the single source assumption, although it is global tight. In this paper, we first derive an explicit ZZB applicable for hybrid coherent/incoherent multiple sources DOA estimation. In detail, we incorporate Woodbury matrix identity and Sylvester's determinant theorem to generalize the ZZB from single source DOA estimation to multiple sources DOA estimation, which, unfortunately, becomes invalid when it is far away from the asymptotic region. We then introduce the order statistics to describe the effect of ordering process during MSE calculation on the change of a priori distribution of DOAs, such that the derived ZZB can keep a tight bound on the MSE outside the asymptotic region. The derived ZZB is for the first time formulated as the function of the coherent coefficients between the coherent sources, and reveals the relationship between the MSE convergency in the a priori performance region and the number of sources. Moreover, the derived ZZB also provides a unified tight bound for both overdetermined DOAs estimation and underdetermined DOAs estimation. Simulation results demonstrate the obvious advantages of the derived ZZB over the CRB on evaluating and predicting the estimation performance of multiple sources DOA.