Chronosymbolic Learning: Efficient CHC Solving with Symbolic Reasoning and Inductive Learning

Solving Constrained Horn Clauses (CHCs) is a fundamental challenge behind a wide range of verification and analysis tasks. Data-driven approaches show great promise in improving CHC solving without the painstaking manual effort of creating and tuning various heuristics. However, a large performance gap exists between data-driven CHC solvers and symbolic reasoning-based solvers. In this work, we develop a simple but effective framework, "Chronosymbolic Learning", which unifies symbolic information and numerical data points to solve a CHC system efficiently. We also present a simple instance of Chronosymbolic Learning with a data-driven learner and a BMC-styled reasoner. Despite its great simplicity, experimental results show the efficacy and robustness of our tool. It outperforms state-of-the-art CHC solvers on a dataset consisting of 288 benchmarks, including many instances with non-linear integer arithmetics.

2D+3D facial expression recognition via embedded tensor manifold regularization

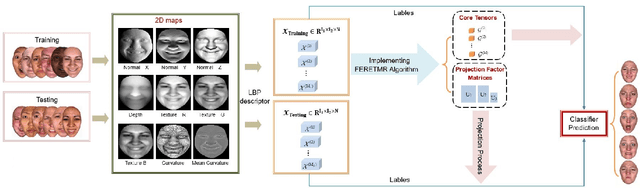
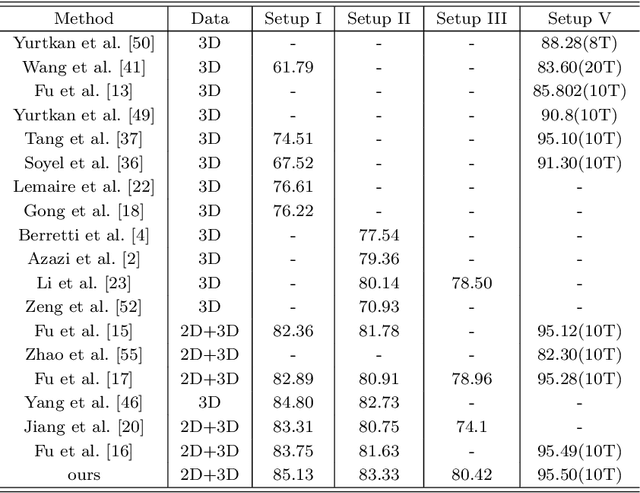
In this paper, a novel approach via embedded tensor manifold regularization for 2D+3D facial expression recognition (FERETMR) is proposed. Firstly, 3D tensors are constructed from 2D face images and 3D face shape models to keep the structural information and correlations. To maintain the local structure (geometric information) of 3D tensor samples in the low-dimensional tensors space during the dimensionality reduction, the $\ell_0$-norm of the core tensors and a tensor manifold regularization scheme embedded on core tensors are adopted via a low-rank truncated Tucker decomposition on the generated tensors. As a result, the obtained factor matrices will be used for facial expression classification prediction. To make the resulting tensor optimization more tractable, $\ell_1$-norm surrogate is employed to relax $\ell_0$-norm and hence the resulting tensor optimization problem has a nonsmooth objective function due to the $\ell_1$-norm and orthogonal constraints from the orthogonal Tucker decomposition. To efficiently tackle this tensor optimization problem, we establish the first-order optimality condition in terms of stationary points, and then design a block coordinate descent (BCD) algorithm with convergence analysis and the computational complexity. Numerical results on BU-3DFE database and Bosphorus databases demonstrate the effectiveness of our proposed approach.

Sparse and Low-Rank Covariance Matrices Estimation

This paper aims at achieving a simultaneously sparse and low-rank estimator from the semidefinite population covariance matrices. We first benefit from a convex optimization which develops $l_1$-norm penalty to encourage the sparsity and nuclear norm to favor the low-rank property. For the proposed estimator, we then prove that with large probability, the Frobenious norm of the estimation rate can be of order $O(\sqrt{s(\log{r})/n})$ under a mild case, where $s$ and $r$ denote the number of sparse entries and the rank of the population covariance respectively, $n$ notes the sample capacity. Finally an efficient alternating direction method of multipliers with global convergence is proposed to tackle this problem, and meantime merits of the approach are also illustrated by practicing numerical simulations.