Yunfang Fu
2D+3D facial expression recognition via embedded tensor manifold regularization
Jan 29, 2022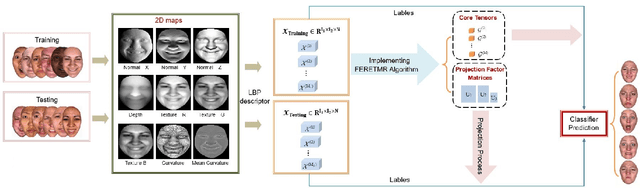


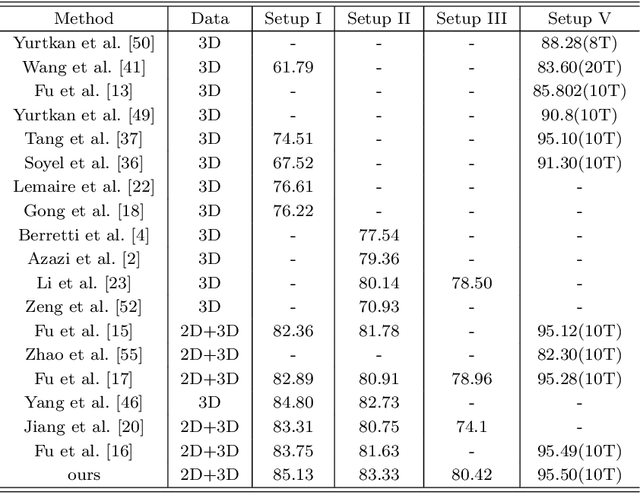
Abstract:In this paper, a novel approach via embedded tensor manifold regularization for 2D+3D facial expression recognition (FERETMR) is proposed. Firstly, 3D tensors are constructed from 2D face images and 3D face shape models to keep the structural information and correlations. To maintain the local structure (geometric information) of 3D tensor samples in the low-dimensional tensors space during the dimensionality reduction, the $\ell_0$-norm of the core tensors and a tensor manifold regularization scheme embedded on core tensors are adopted via a low-rank truncated Tucker decomposition on the generated tensors. As a result, the obtained factor matrices will be used for facial expression classification prediction. To make the resulting tensor optimization more tractable, $\ell_1$-norm surrogate is employed to relax $\ell_0$-norm and hence the resulting tensor optimization problem has a nonsmooth objective function due to the $\ell_1$-norm and orthogonal constraints from the orthogonal Tucker decomposition. To efficiently tackle this tensor optimization problem, we establish the first-order optimality condition in terms of stationary points, and then design a block coordinate descent (BCD) algorithm with convergence analysis and the computational complexity. Numerical results on BU-3DFE database and Bosphorus databases demonstrate the effectiveness of our proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge