LinSATNet: The Positive Linear Satisfiability Neural Networks

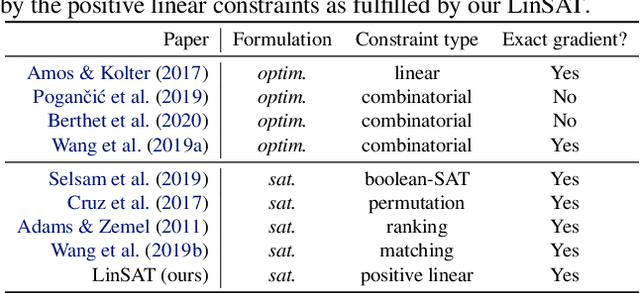
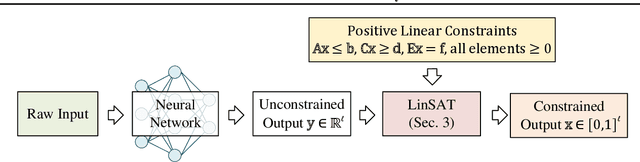
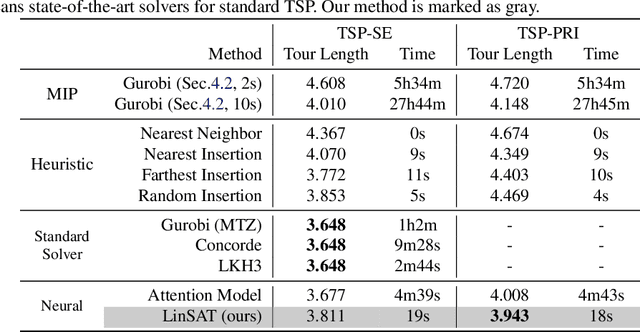
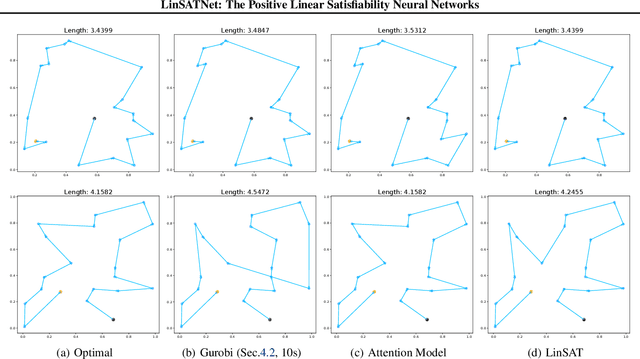
Encoding constraints into neural networks is attractive. This paper studies how to introduce the popular positive linear satisfiability to neural networks. We propose the first differentiable satisfiability layer based on an extension of the classic Sinkhorn algorithm for jointly encoding multiple sets of marginal distributions. We further theoretically characterize the convergence property of the Sinkhorn algorithm for multiple marginals. In contrast to the sequential decision e.g.\ reinforcement learning-based solvers, we showcase our technique in solving constrained (specifically satisfiability) problems by one-shot neural networks, including i) a neural routing solver learned without supervision of optimal solutions; ii) a partial graph matching network handling graphs with unmatchable outliers on both sides; iii) a predictive network for financial portfolios with continuous constraints. To our knowledge, there exists no one-shot neural solver for these scenarios when they are formulated as satisfiability problems. Source code is available at https://github.com/Thinklab-SJTU/LinSATNet

BiasedWalk: Learning Global-aware Node Embeddings via Biased Sampling

Popular node embedding methods such as DeepWalk follow the paradigm of performing random walks on the graph, and then requiring each node to be proximate to those appearing along with it. Though proved to be successful in various tasks, this paradigm reduces a graph with topology to a set of sequential sentences, thus omitting global information. To produce global-aware node embeddings, we propose BiasedWalk, a biased random walk strategy that favors nodes with similar semantics. Empirical evidence suggests BiasedWalk can generally enhance global awareness of the generated embeddings.