OptMetaOpenFOAM: Large Language Model Driven Chain of Thought for Sensitivity Analysis and Parameter Optimization based on CFD

Merging natural language interfaces with computational fluid dynamics (CFD) workflows presents transformative opportunities for both industry and research. In this study, we introduce OptMetaOpenFOAM - a novel framework that bridges MetaOpenFOAM with external analysis and optimization tool libraries through a large language model (LLM)-driven chain-of-thought (COT) methodology. By automating complex CFD tasks via natural language inputs, the framework empowers non-expert users to perform sensitivity analyses and parameter optimizations with markedly improved efficiency. The test dataset comprises 11 distinct CFD analysis or optimization tasks, including a baseline simulation task derived from an OpenFOAM tutorial covering fluid dynamics, combustion, and heat transfer. Results confirm that OptMetaOpenFOAM can accurately interpret user requirements expressed in natural language and effectively invoke external tool libraries alongside MetaOpenFOAM to complete the tasks. Furthermore, validation on a non-OpenFOAM tutorial case - namely, a hydrogen combustion chamber - demonstrates that a mere 200-character natural language input can trigger a sequence of simulation, postprocessing, analysis, and optimization tasks spanning over 2,000 lines of code. These findings underscore the transformative potential of LLM-driven COT methodologies in linking external tool for advanced analysis and optimization, positioning OptMetaOpenFOAM as an effective tool that streamlines CFD simulations and enhances their convenience and efficiency for both industrial and research applications. Code is available at https://github.com/Terry-cyx/MetaOpenFOAM.

Arrhenius.jl: A Differentiable Combustion SimulationPackage

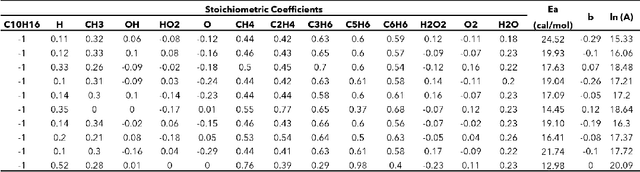
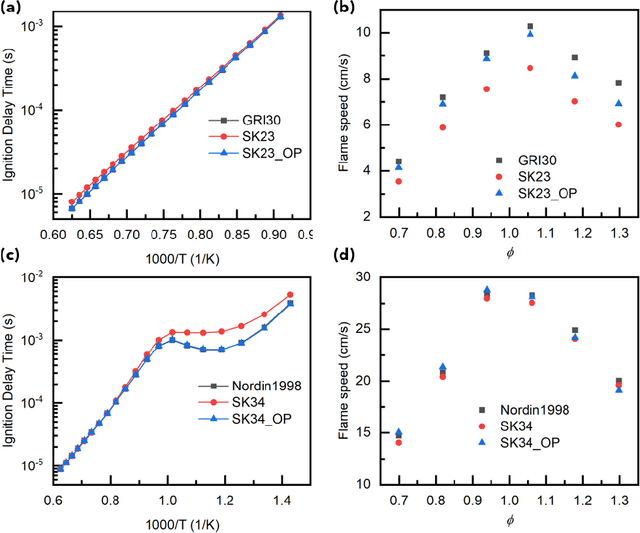
Combustion kinetic modeling is an integral part of combustion simulation, and extensive studies have been devoted to developing both high fidelity and computationally affordable models. Despite these efforts, modeling combustion kinetics is still challenging due to the demand for expert knowledge and optimization against experiments, as well as the lack of understanding of the associated uncertainties. Therefore, data-driven approaches that enable efficient discovery and calibration of kinetic models have received much attention in recent years, the core of which is the optimization based on big data. Differentiable programming is a promising approach for learning kinetic models from data by efficiently computing the gradient of objective functions to model parameters. However, it is often challenging to implement differentiable programming in practice. Therefore, it is still not available in widely utilized combustion simulation packages such as CHEMKIN and Cantera. Here, we present a differentiable combustion simulation package leveraging the eco-system in Julia, including DifferentialEquations.jl for solving differential equations, ForwardDiff.jl for auto-differentiation, and Flux.jl for incorporating neural network models into combustion simulations and optimizing neural network models using the state-of-the-art deep learning optimizers. We demonstrate the benefits of differentiable programming in efficient and accurate gradient computations, with applications in uncertainty quantification, kinetic model reduction, data assimilation, and model discovery.

Uncertainty Propagation in Deep Neural Network Using Active Subspace

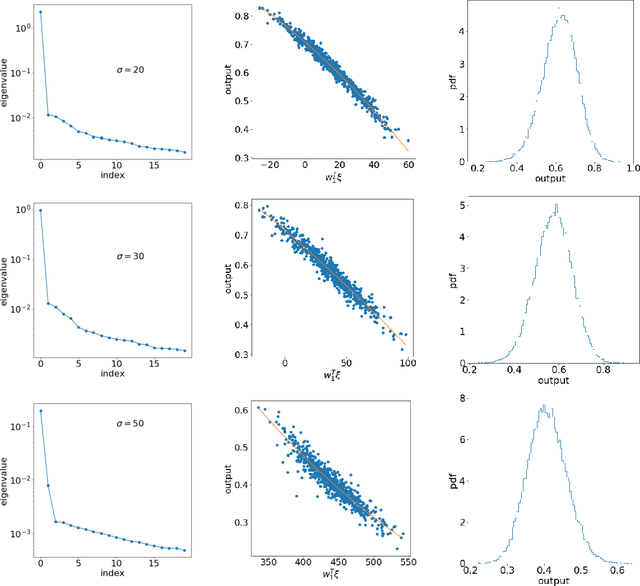
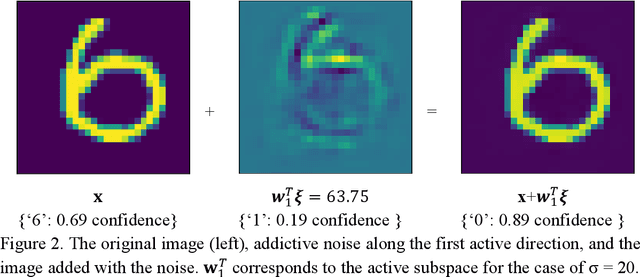
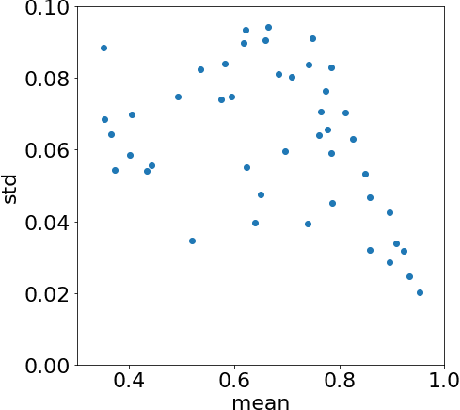
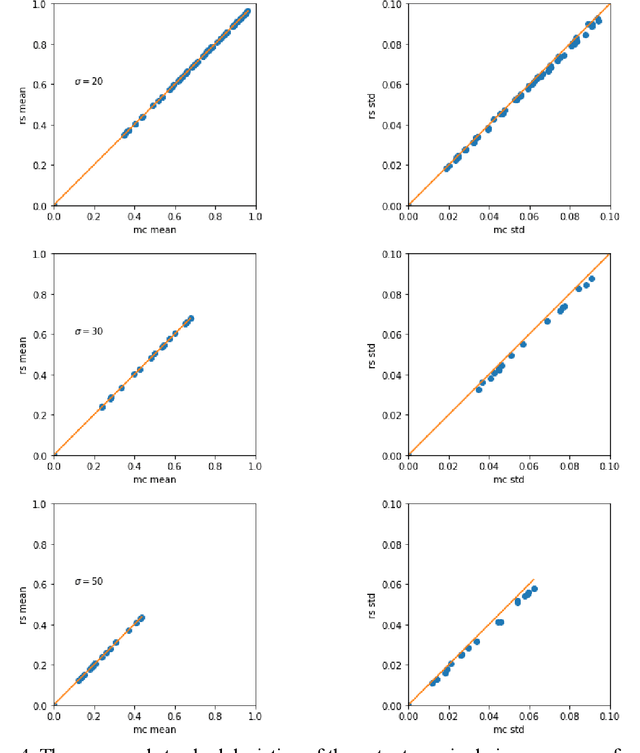
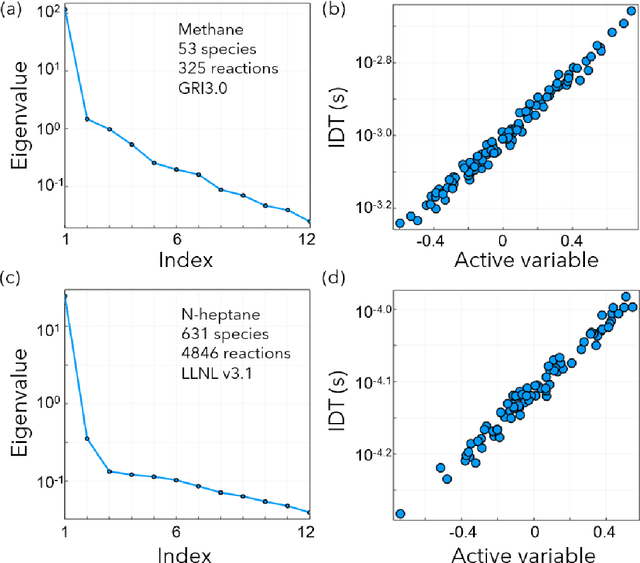
The inputs of deep neural network (DNN) from real-world data usually come with uncertainties. Yet, it is challenging to propagate the uncertainty in the input features to the DNN predictions at a low computational cost. This work employs a gradient-based subspace method and response surface technique to accelerate the uncertainty propagation in DNN. Specifically, the active subspace method is employed to identify the most important subspace in the input features using the gradient of the DNN output to the inputs. Then the response surface within that low-dimensional subspace can be efficiently built, and the uncertainty of the prediction can be acquired by evaluating the computationally cheap response surface instead of the DNN models. In addition, the subspace can help explain the adversarial examples. The approach is demonstrated in MNIST datasets with a convolutional neural network.