Sili Deng
Learning continuous SOC-dependent thermal decomposition kinetics for Li-ion cathodes using KA-CRNNs
Dec 17, 2025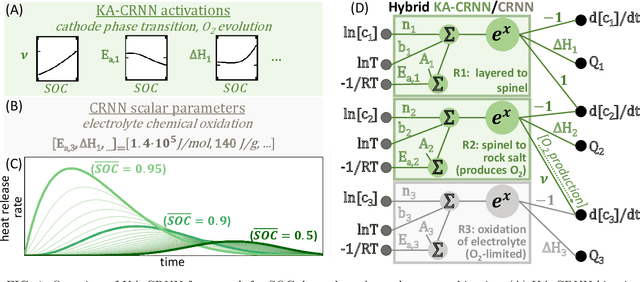
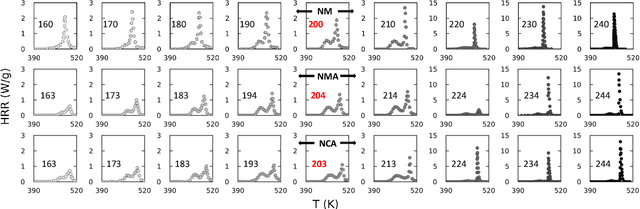
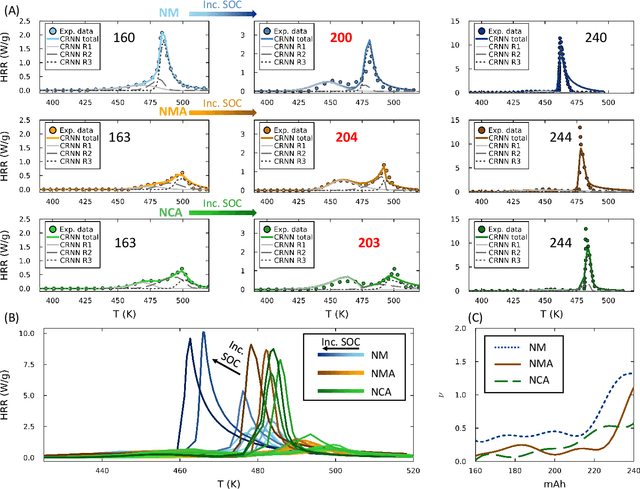
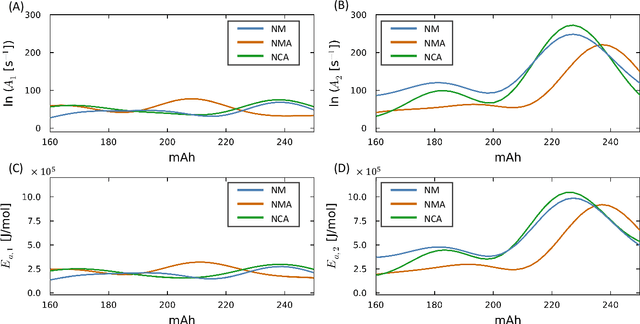
Abstract:Thermal runaway in lithium-ion batteries is strongly influenced by the state of charge (SOC). Existing predictive models typically infer scalar kinetic parameters at a full SOC or a few discrete SOC levels, preventing them from capturing the continuous SOC dependence that governs exothermic behavior during abuse conditions. To address this, we apply the Kolmogorov-Arnold Chemical Reaction Neural Network (KA-CRNN) framework to learn continuous and realistic SOC-dependent exothermic cathode-electrolyte interactions. We apply a physics-encoded KA-CRNN to learn SOC-dependent kinetic parameters for cathode-electrolyte decomposition directly from differential scanning calorimetry (DSC) data. A mechanistically informed reaction pathway is embedded into the network architecture, enabling the activation energies, pre-exponential factors, enthalpies, and related parameters to be represented as continuous and fully interpretable functions of the SOC. The framework is demonstrated for NCA, NM, and NMA cathodes, yielding models that reproduce DSC heat-release features across all SOCs and provide interpretable insight into SOC-dependent oxygen-release and phase-transformation mechanisms. This approach establishes a foundation for extending kinetic parameter dependencies to additional environmental and electrochemical variables, supporting more accurate and interpretable thermal-runaway prediction and monitoring.
Kolmogorov-Arnold Chemical Reaction Neural Networks for learning pressure-dependent kinetic rate laws
Nov 10, 2025Abstract:Chemical Reaction Neural Networks (CRNNs) have emerged as an interpretable machine learning framework for discovering reaction kinetics directly from data, while strictly adhering to the Arrhenius and mass action laws. However, standard CRNNs cannot represent pressure-dependent rate behavior, which is critical in many combustion and chemical systems and typically requires empirical formulations such as Troe or PLOG. Here, we develop Kolmogorov-Arnold Chemical Reaction Neural Networks (KA-CRNNs) that generalize CRNNs by modeling each kinetic parameter as a learnable function of system pressure using Kolmogorov-Arnold activations. This structure maintains full interpretability and physical consistency while enabling assumption-free inference of pressure effects directly from data. A proof-of-concept study on the CH3 recombination reaction demonstrates that KA-CRNNs accurately reproduce pressure-dependent kinetics across a range of temperatures and pressures, outperforming conventional interpolative models. The framework establishes a foundation for data-driven discovery of extended kinetic behaviors in complex reacting systems, advancing interpretable and physics-consistent approaches for chemical model inference.
ChemKANs for Combustion Chemistry Modeling and Acceleration
Apr 17, 2025



Abstract:Efficient chemical kinetic model inference and application for combustion problems is challenging due to large ODE systems and wideley separated time scales. Machine learning techniques have been proposed to streamline these models, though strong nonlinearity and numerical stiffness combined with noisy data sources makes their application challenging. The recently developed Kolmogorov-Arnold Networks (KANs) and KAN ordinary differential equations (KAN-ODEs) have been demonstrated as powerful tools for scientific applications thanks to their rapid neural scaling, improved interpretability, and smooth activation functions. Here, we develop ChemKANs by augmenting the KAN-ODE framework with physical knowledge of the flow of information through the relevant kinetic and thermodynamic laws, as well as an elemental conservation loss term. This novel framework encodes strong inductive bias that enables streamlined training and higher accuracy predictions, while facilitating parameter sparsity through full sharing of information across all inputs and outputs. In a model inference investigation, we find that ChemKANs exhibit no overfitting or model degradation when tasked with extracting predictive models from data that is both sparse and noisy, a task that a standard DeepONet struggles to accomplish. Next, we find that a remarkably parameter-lean ChemKAN (only 344 parameters) can accurately represent hydrogen combustion chemistry, providing a 2x acceleration over the detailed chemistry in a solver that is generalizable to larger-scale turbulent flow simulations. These demonstrations indicate potential for ChemKANs in combustion physics and chemical kinetics, and demonstrate the scalability of generic KAN-ODEs in significantly larger and more numerically challenging problems than previously studied.
LeanKAN: A Parameter-Lean Kolmogorov-Arnold Network Layer with Improved Memory Efficiency and Convergence Behavior
Feb 25, 2025Abstract:The recently proposed Kolmogorov-Arnold network (KAN) is a promising alternative to multi-layer perceptrons (MLPs) for data-driven modeling. While original KAN layers were only capable of representing the addition operator, the recently-proposed MultKAN layer combines addition and multiplication subnodes in an effort to improve representation performance. Here, we find that MultKAN layers suffer from a few key drawbacks including limited applicability in output layers, bulky parameterizations with extraneous activations, and the inclusion of complex hyperparameters. To address these issues, we propose LeanKANs, a direct and modular replacement for MultKAN and traditional AddKAN layers. LeanKANs address these three drawbacks of MultKAN through general applicability as output layers, significantly reduced parameter counts for a given network structure, and a smaller set of hyperparameters. As a one-to-one layer replacement for standard AddKAN and MultKAN layers, LeanKAN is able to provide these benefits to traditional KAN learning problems as well as augmented KAN structures in which it serves as the backbone, such as KAN Ordinary Differential Equations (KAN-ODEs) or Deep Operator KANs (DeepOKAN). We demonstrate LeanKAN's simplicity and efficiency in a series of demonstrations carried out across both a standard KAN toy problem and a KAN-ODE dynamical system modeling problem, where we find that its sparser parameterization and compact structure serve to increase its expressivity and learning capability, leading it to outperform similar and even much larger MultKANs in various tasks.
KAN-ODEs: Kolmogorov-Arnold Network Ordinary Differential Equations for Learning Dynamical Systems and Hidden Physics
Jul 05, 2024



Abstract:Kolmogorov-Arnold Networks (KANs) as an alternative to Multi-layer perceptrons (MLPs) are a recent development demonstrating strong potential for data-driven modeling. This work applies KANs as the backbone of a Neural Ordinary Differential Equation framework, generalizing their use to the time-dependent and grid-sensitive cases often seen in scientific machine learning applications. The proposed KAN-ODEs retain the flexible dynamical system modeling framework of Neural ODEs while leveraging the many benefits of KANs, including faster neural scaling, stronger interpretability, and lower parameter counts when compared against MLPs. We demonstrate these benefits in three test cases: the Lotka-Volterra predator-prey model, Burgers' equation, and the Fisher-KPP PDE. We showcase the strong performance of parameter-lean KAN-ODE systems generally in reconstructing entire dynamical systems, and also in targeted applications to the inference of a source term in an otherwise known flow field. We additionally demonstrate the interpretability of KAN-ODEs via activation function visualization and symbolic regression of trained results. The successful training of KAN-ODEs and their improved performance when compared to traditional Neural ODEs implies significant potential in leveraging this novel network architecture in myriad scientific machine learning applications.
Arrhenius.jl: A Differentiable Combustion SimulationPackage
Jun 19, 2021
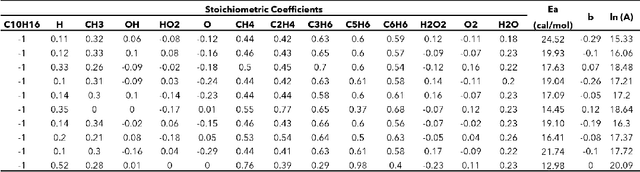
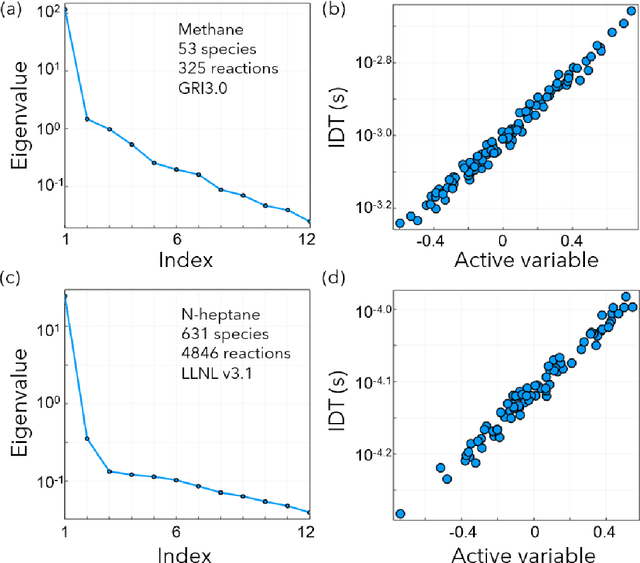
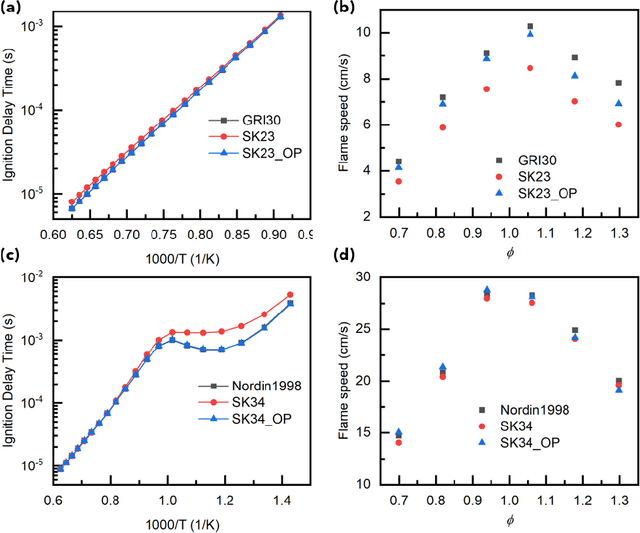
Abstract:Combustion kinetic modeling is an integral part of combustion simulation, and extensive studies have been devoted to developing both high fidelity and computationally affordable models. Despite these efforts, modeling combustion kinetics is still challenging due to the demand for expert knowledge and optimization against experiments, as well as the lack of understanding of the associated uncertainties. Therefore, data-driven approaches that enable efficient discovery and calibration of kinetic models have received much attention in recent years, the core of which is the optimization based on big data. Differentiable programming is a promising approach for learning kinetic models from data by efficiently computing the gradient of objective functions to model parameters. However, it is often challenging to implement differentiable programming in practice. Therefore, it is still not available in widely utilized combustion simulation packages such as CHEMKIN and Cantera. Here, we present a differentiable combustion simulation package leveraging the eco-system in Julia, including DifferentialEquations.jl for solving differential equations, ForwardDiff.jl for auto-differentiation, and Flux.jl for incorporating neural network models into combustion simulations and optimizing neural network models using the state-of-the-art deep learning optimizers. We demonstrate the benefits of differentiable programming in efficient and accurate gradient computations, with applications in uncertainty quantification, kinetic model reduction, data assimilation, and model discovery.
Autonomous Kinetic Modeling of Biomass Pyrolysis using Chemical Reaction Neural Networks
May 24, 2021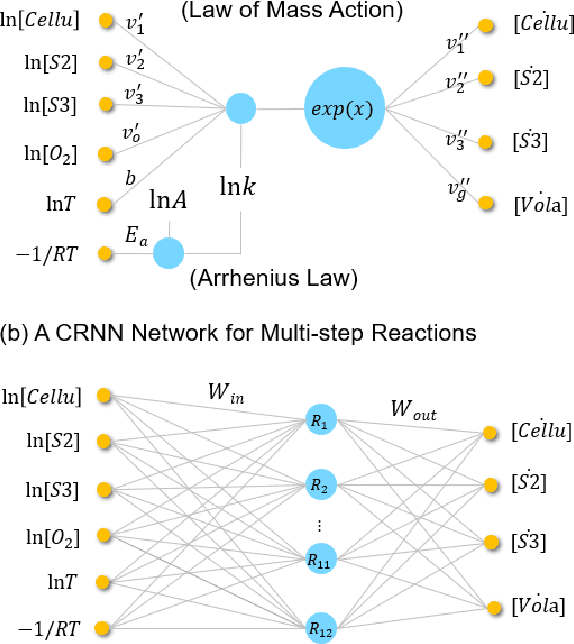
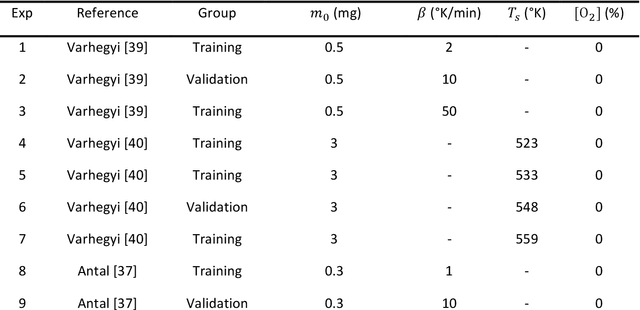
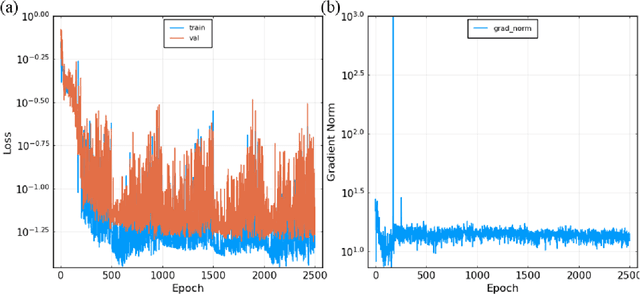
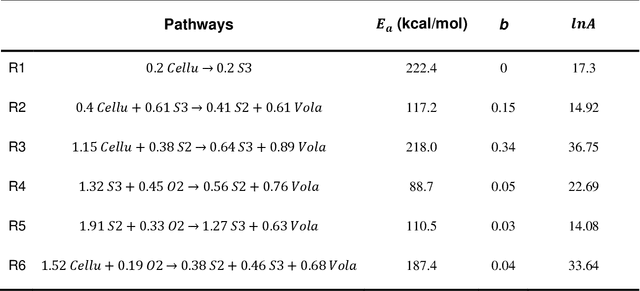
Abstract:Modeling the burning processes of biomass such as wood, grass, and crops is crucial for the modeling and prediction of wildland and urban fire behavior. Despite its importance, the burning of solid fuels remains poorly understood, which can be partly attributed to the unknown chemical kinetics of most solid fuels. Most available kinetic models were built upon expert knowledge, which requires chemical insights and years of experience. This work presents a framework for autonomously discovering biomass pyrolysis kinetic models from thermogravimetric analyzer (TGA) experimental data using the recently developed chemical reaction neural networks (CRNN). The approach incorporated the CRNN model into the framework of neural ordinary differential equations to predict the residual mass in TGA data. In addition to the flexibility of neural-network-based models, the learned CRNN model is fully interpretable, by incorporating the fundamental physics laws, such as the law of mass action and Arrhenius law, into the neural network structure. The learned CRNN model can then be translated into the classical forms of biomass chemical kinetic models, which facilitates the extraction of chemical insights and the integration of the kinetic model into large-scale fire simulations. We demonstrated the effectiveness of the framework in predicting the pyrolysis and oxidation of cellulose. This successful demonstration opens the possibility of rapid and autonomous chemical kinetic modeling of solid fuels, such as wildfire fuels and industrial polymers.
Inference of cell dynamics on perturbation data using adjoint sensitivity
Apr 13, 2021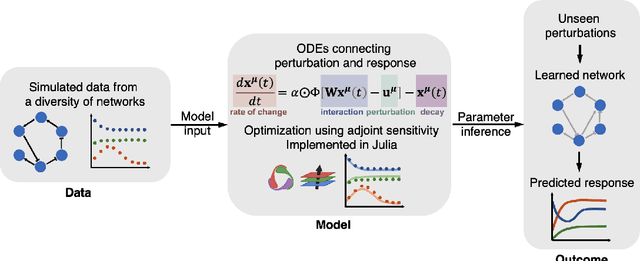
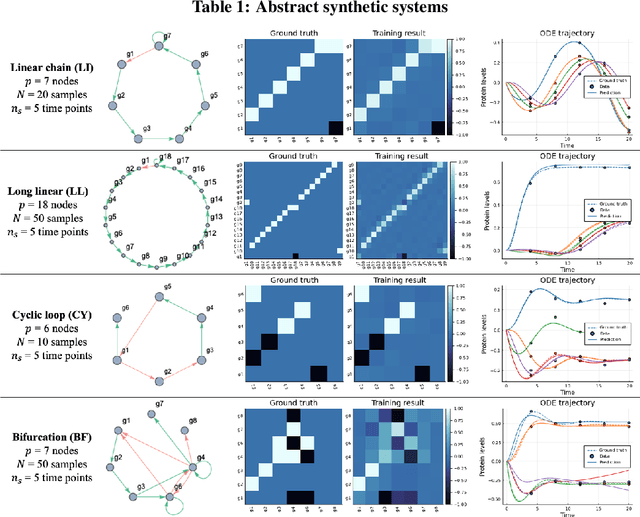
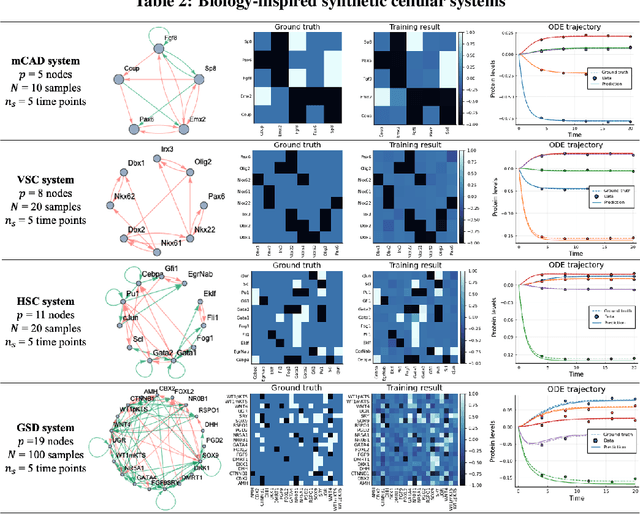
Abstract:Data-driven dynamic models of cell biology can be used to predict cell response to unseen perturbations. Recent work (CellBox) had demonstrated the derivation of interpretable models with explicit interaction terms, in which the parameters were optimized using machine learning techniques. While the previous work was tested only in a single biological setting, this work aims to extend the range of applicability of this model inference approach to a diversity of biological systems. Here we adapted CellBox in Julia differential programming and augmented the method with adjoint algorithms, which has recently been used in the context of neural ODEs. We trained the models using simulated data from both abstract and biology-inspired networks, which afford the ability to evaluate the recovery of the ground truth network structure. The resulting accuracy of prediction by these models is high both in terms of low error against data and excellent agreement with the network structure used for the simulated training data. While there is no analogous ground truth for real life biological systems, this work demonstrates the ability to construct and parameterize a considerable diversity of network models with high predictive ability. The expectation is that this kind of procedure can be used on real perturbation-response data to derive models applicable to diverse biological systems.
Stiff Neural Ordinary Differential Equations
Mar 29, 2021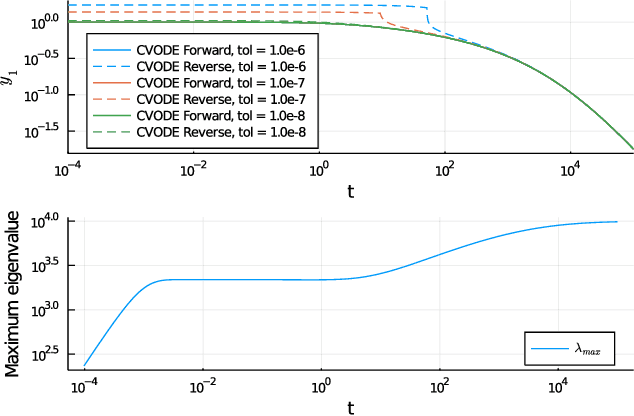
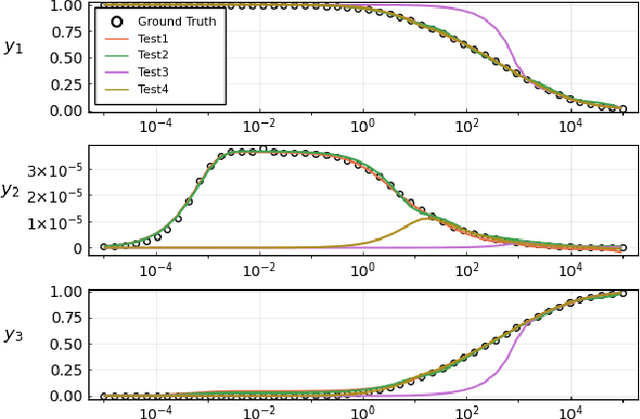
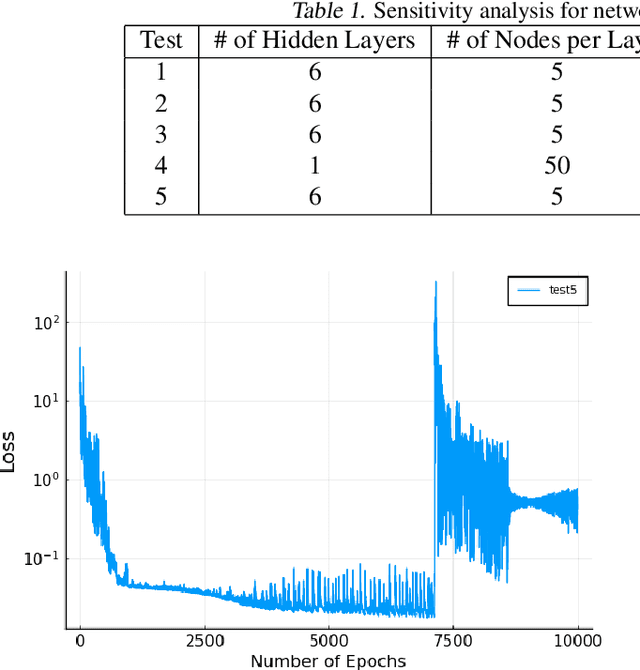
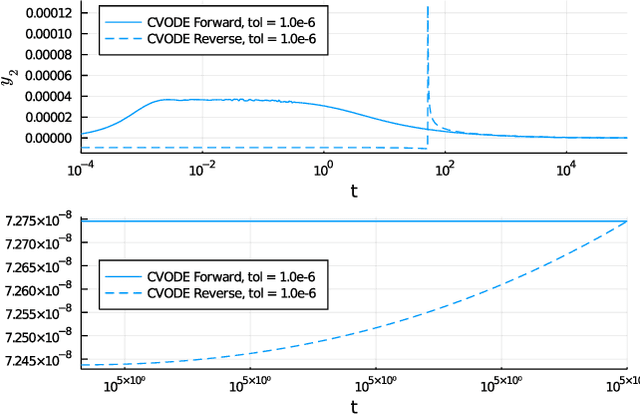
Abstract:Neural Ordinary Differential Equations (ODE) are a promising approach to learn dynamic models from time-series data in science and engineering applications. This work aims at learning Neural ODE for stiff systems, which are usually raised from chemical kinetic modeling in chemical and biological systems. We first show the challenges of learning neural ODE in the classical stiff ODE systems of Robertson's problem and propose techniques to mitigate the challenges associated with scale separations in stiff systems. We then present successful demonstrations in stiff systems of Robertson's problem and an air pollution problem. The demonstrations show that the usage of deep networks with rectified activations, proper scaling of the network outputs as well as loss functions, and stabilized gradient calculations are the key techniques enabling the learning of stiff neural ODE. The success of learning stiff neural ODE opens up possibilities of using neural ODEs in applications with widely varying time-scales, like chemical dynamics in energy conversion, environmental engineering, and the life sciences.
Autonomous Discovery of Unknown Reaction Pathways from Data by Chemical Reaction Neural Network
Feb 20, 2020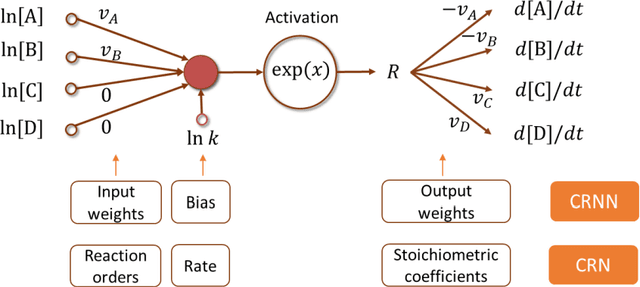
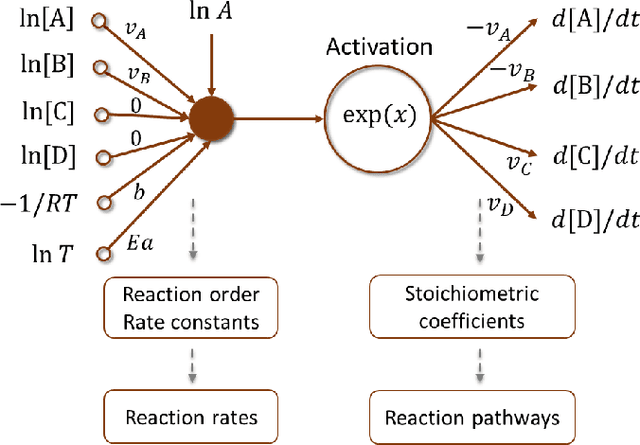
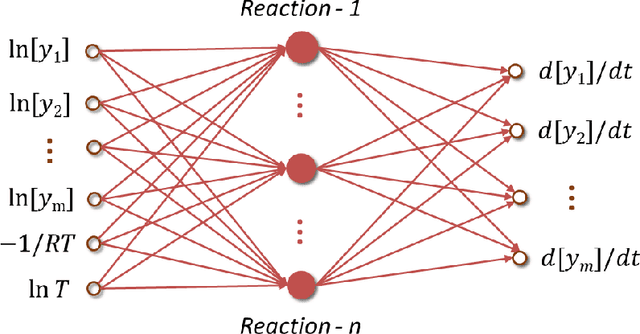
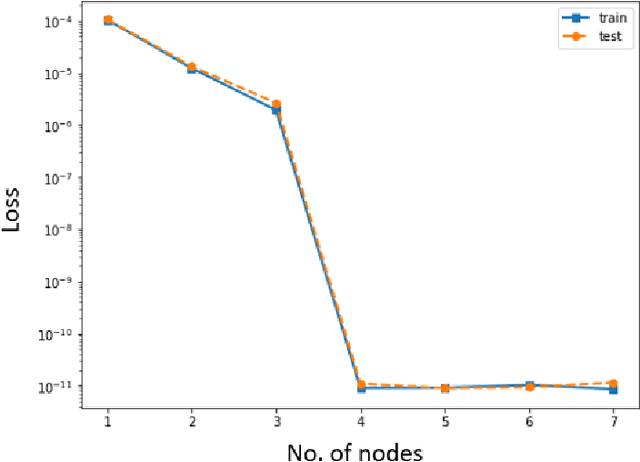
Abstract:The inference of chemical reaction networks is an important task in understanding the chemical processes in life sciences and environment. Yet, only a few reaction systems are well-understood due to a large number of important reaction pathways involved but still unknown. Revealing unknown reaction pathways is an important task for scientific discovery that takes decades and requires lots of expert knowledge. This work presents a neural network approach for discovering unknown reaction pathways from concentration time series data. The neural network denoted as Chemical Reaction Neural Network (CRNN), is designed to be equivalent to chemical reaction networks by following the fundamental physics laws of the Law of Mass Action and Arrhenius Law. The CRNN is physically interpretable, and its weights correspond to the reaction pathways and rate constants of the chemical reaction network. Then, inferencing the reaction pathways and the rate constants are accomplished by training the equivalent CRNN via stochastic gradient descent. The approach precludes the need for expert knowledge in proposing candidate reactions, such that the inference is autonomous and applicable to new systems for which there is no existing empirical knowledge to propose reaction pathways. The physical interpretability also makes the CRNN not only capable of fitting the data for a given system but also developing knowledge of unknown pathways that could be generalized to similar chemical systems. Finally, the approach is applied to several chemical systems in chemical engineering and biochemistry to demonstrate its robustness and generality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge