ChemKANs for Combustion Chemistry Modeling and Acceleration

Efficient chemical kinetic model inference and application for combustion problems is challenging due to large ODE systems and wideley separated time scales. Machine learning techniques have been proposed to streamline these models, though strong nonlinearity and numerical stiffness combined with noisy data sources makes their application challenging. The recently developed Kolmogorov-Arnold Networks (KANs) and KAN ordinary differential equations (KAN-ODEs) have been demonstrated as powerful tools for scientific applications thanks to their rapid neural scaling, improved interpretability, and smooth activation functions. Here, we develop ChemKANs by augmenting the KAN-ODE framework with physical knowledge of the flow of information through the relevant kinetic and thermodynamic laws, as well as an elemental conservation loss term. This novel framework encodes strong inductive bias that enables streamlined training and higher accuracy predictions, while facilitating parameter sparsity through full sharing of information across all inputs and outputs. In a model inference investigation, we find that ChemKANs exhibit no overfitting or model degradation when tasked with extracting predictive models from data that is both sparse and noisy, a task that a standard DeepONet struggles to accomplish. Next, we find that a remarkably parameter-lean ChemKAN (only 344 parameters) can accurately represent hydrogen combustion chemistry, providing a 2x acceleration over the detailed chemistry in a solver that is generalizable to larger-scale turbulent flow simulations. These demonstrations indicate potential for ChemKANs in combustion physics and chemical kinetics, and demonstrate the scalability of generic KAN-ODEs in significantly larger and more numerically challenging problems than previously studied.

LeanKAN: A Parameter-Lean Kolmogorov-Arnold Network Layer with Improved Memory Efficiency and Convergence Behavior

The recently proposed Kolmogorov-Arnold network (KAN) is a promising alternative to multi-layer perceptrons (MLPs) for data-driven modeling. While original KAN layers were only capable of representing the addition operator, the recently-proposed MultKAN layer combines addition and multiplication subnodes in an effort to improve representation performance. Here, we find that MultKAN layers suffer from a few key drawbacks including limited applicability in output layers, bulky parameterizations with extraneous activations, and the inclusion of complex hyperparameters. To address these issues, we propose LeanKANs, a direct and modular replacement for MultKAN and traditional AddKAN layers. LeanKANs address these three drawbacks of MultKAN through general applicability as output layers, significantly reduced parameter counts for a given network structure, and a smaller set of hyperparameters. As a one-to-one layer replacement for standard AddKAN and MultKAN layers, LeanKAN is able to provide these benefits to traditional KAN learning problems as well as augmented KAN structures in which it serves as the backbone, such as KAN Ordinary Differential Equations (KAN-ODEs) or Deep Operator KANs (DeepOKAN). We demonstrate LeanKAN's simplicity and efficiency in a series of demonstrations carried out across both a standard KAN toy problem and a KAN-ODE dynamical system modeling problem, where we find that its sparser parameterization and compact structure serve to increase its expressivity and learning capability, leading it to outperform similar and even much larger MultKANs in various tasks.

KAN-ODEs: Kolmogorov-Arnold Network Ordinary Differential Equations for Learning Dynamical Systems and Hidden Physics

Kolmogorov-Arnold Networks (KANs) as an alternative to Multi-layer perceptrons (MLPs) are a recent development demonstrating strong potential for data-driven modeling. This work applies KANs as the backbone of a Neural Ordinary Differential Equation framework, generalizing their use to the time-dependent and grid-sensitive cases often seen in scientific machine learning applications. The proposed KAN-ODEs retain the flexible dynamical system modeling framework of Neural ODEs while leveraging the many benefits of KANs, including faster neural scaling, stronger interpretability, and lower parameter counts when compared against MLPs. We demonstrate these benefits in three test cases: the Lotka-Volterra predator-prey model, Burgers' equation, and the Fisher-KPP PDE. We showcase the strong performance of parameter-lean KAN-ODE systems generally in reconstructing entire dynamical systems, and also in targeted applications to the inference of a source term in an otherwise known flow field. We additionally demonstrate the interpretability of KAN-ODEs via activation function visualization and symbolic regression of trained results. The successful training of KAN-ODEs and their improved performance when compared to traditional Neural ODEs implies significant potential in leveraging this novel network architecture in myriad scientific machine learning applications.

Stiff Neural Ordinary Differential Equations

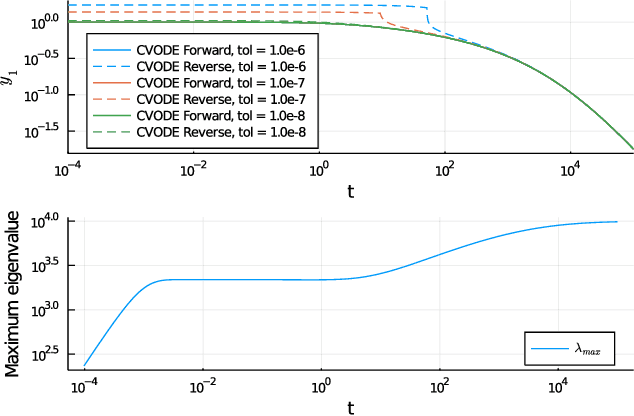
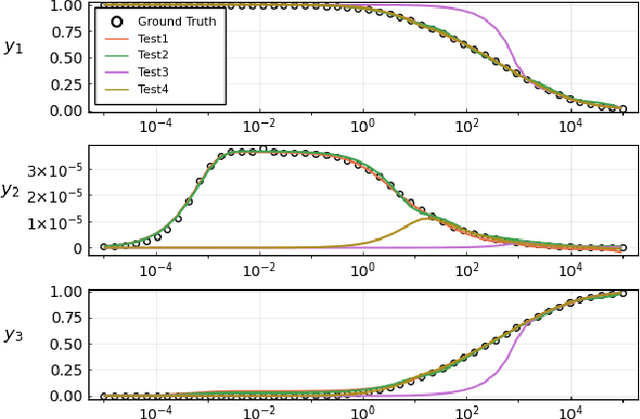
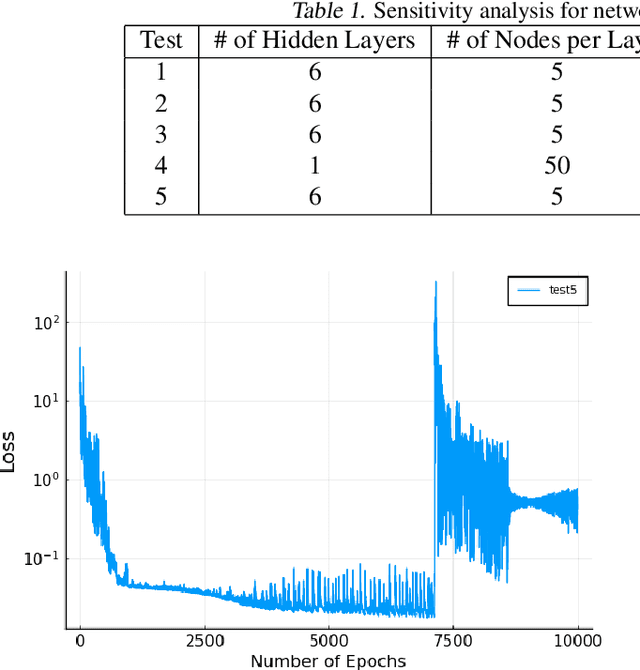
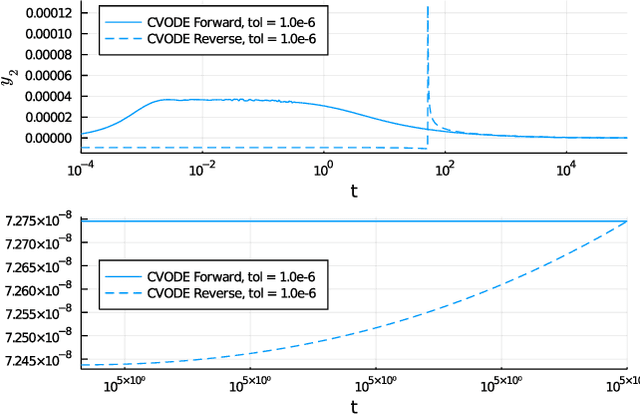
Neural Ordinary Differential Equations (ODE) are a promising approach to learn dynamic models from time-series data in science and engineering applications. This work aims at learning Neural ODE for stiff systems, which are usually raised from chemical kinetic modeling in chemical and biological systems. We first show the challenges of learning neural ODE in the classical stiff ODE systems of Robertson's problem and propose techniques to mitigate the challenges associated with scale separations in stiff systems. We then present successful demonstrations in stiff systems of Robertson's problem and an air pollution problem. The demonstrations show that the usage of deep networks with rectified activations, proper scaling of the network outputs as well as loss functions, and stabilized gradient calculations are the key techniques enabling the learning of stiff neural ODE. The success of learning stiff neural ODE opens up possibilities of using neural ODEs in applications with widely varying time-scales, like chemical dynamics in energy conversion, environmental engineering, and the life sciences.