Neural Laplacian Operator for 3D Point Clouds

The discrete Laplacian operator holds a crucial role in 3D geometry processing, yet it is still challenging to define it on point clouds. Previous works mainly focused on constructing a local triangulation around each point to approximate the underlying manifold for defining the Laplacian operator, which may not be robust or accurate. In contrast, we simply use the K-nearest neighbors (KNN) graph constructed from the input point cloud and learn the Laplacian operator on the KNN graph with graph neural networks (GNNs). However, the ground-truth Laplacian operator is defined on a manifold mesh with a different connectivity from the KNN graph and thus cannot be directly used for training. To train the GNN, we propose a novel training scheme by imitating the behavior of the ground-truth Laplacian operator on a set of probe functions so that the learned Laplacian operator behaves similarly to the ground-truth Laplacian operator. We train our network on a subset of ShapeNet and evaluate it across a variety of point clouds. Compared with previous methods, our method reduces the error by an order of magnitude and excels in handling sparse point clouds with thin structures or sharp features. Our method also demonstrates a strong generalization ability to unseen shapes. With our learned Laplacian operator, we further apply a series of Laplacian-based geometry processing algorithms directly to point clouds and achieve accurate results, enabling many exciting possibilities for geometry processing on point clouds. The code and trained models are available at https://github.com/IntelligentGeometry/NeLo.

RPBG: Towards Robust Neural Point-based Graphics in the Wild

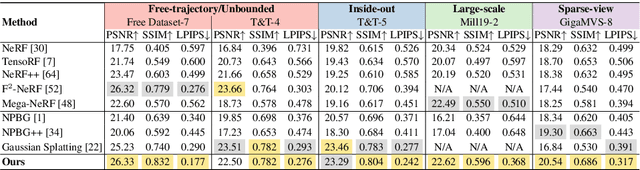
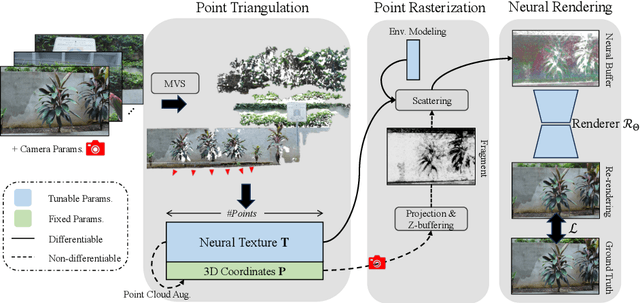
Point-based representations have recently gained popularity in novel view synthesis, for their unique advantages, e.g., intuitive geometric representation, simple manipulation, and faster convergence. However, based on our observation, these point-based neural re-rendering methods are only expected to perform well under ideal conditions and suffer from noisy, patchy points and unbounded scenes, which are challenging to handle but defacto common in real applications. To this end, we revisit one such influential method, known as Neural Point-based Graphics (NPBG), as our baseline, and propose Robust Point-based Graphics (RPBG). We in-depth analyze the factors that prevent NPBG from achieving satisfactory renderings on generic datasets, and accordingly reform the pipeline to make it more robust to varying datasets in-the-wild. Inspired by the practices in image restoration, we greatly enhance the neural renderer to enable the attention-based correction of point visibility and the inpainting of incomplete rasterization, with only acceptable overheads. We also seek for a simple and lightweight alternative for environment modeling and an iterative method to alleviate the problem of poor geometry. By thorough evaluation on a wide range of datasets with different shooting conditions and camera trajectories, RPBG stably outperforms the baseline by a large margin, and exhibits its great robustness over state-of-the-art NeRF-based variants. Code available at https://github.com/QT-Zhu/RPBG.

Learning the Geodesic Embedding with Graph Neural Networks

We present GeGnn, a learning-based method for computing the approximate geodesic distance between two arbitrary points on discrete polyhedra surfaces with constant time complexity after fast precomputation. Previous relevant methods either focus on computing the geodesic distance between a single source and all destinations, which has linear complexity at least or require a long precomputation time. Our key idea is to train a graph neural network to embed an input mesh into a high-dimensional embedding space and compute the geodesic distance between a pair of points using the corresponding embedding vectors and a lightweight decoding function. To facilitate the learning of the embedding, we propose novel graph convolution and graph pooling modules that incorporate local geodesic information and are verified to be much more effective than previous designs. After training, our method requires only one forward pass of the network per mesh as precomputation. Then, we can compute the geodesic distance between a pair of points using our decoding function, which requires only several matrix multiplications and can be massively parallelized on GPUs. We verify the efficiency and effectiveness of our method on ShapeNet and demonstrate that our method is faster than existing methods by orders of magnitude while achieving comparable or better accuracy. Additionally, our method exhibits robustness on noisy and incomplete meshes and strong generalization ability on out-of-distribution meshes. The code and pretrained model can be found on https://github.com/IntelligentGeometry/GeGnn.