Roadmap to Neuromorphic Computing with Emerging Technologies

The roadmap is organized into several thematic sections, outlining current computing challenges, discussing the neuromorphic computing approach, analyzing mature and currently utilized technologies, providing an overview of emerging technologies, addressing material challenges, exploring novel computing concepts, and finally examining the maturity level of emerging technologies while determining the next essential steps for their advancement.

Extremely-Fast, Energy-Efficient Massive MIMO Precoding with Analog RRAM Matrix Computing

Signal processing in wireless communications, such as precoding, detection, and channel estimation, are basically about solving inverse matrix problems, which, however, are slow and inefficient in conventional digital computers, thus requiring a radical paradigm shift to achieve fast, real-time solutions. Here, for the first time, we apply the emerging analog matrix computing (AMC) to the linear precoding of massive MIMO. The real-valued AMC concept is extended to process complex-valued signals. In order to adapt the MIMO channel models to RRAM conductance mapping, a new matrix inversion circuit is developed. In addition, fully analog dataflow and optimized operational amplifiers are designed to support AMC precoding implementation. Simulation results show that the zero-forcing precoding is solved within 20 ns for a 16x128 MIMO system, which is two orders of magnitude faster than the conventional digital approach. Meanwhile, the energy efficiency is improved by 50x.

Tutorial: Analog Matrix Computing (AMC) with Crosspoint Resistive Memory Arrays

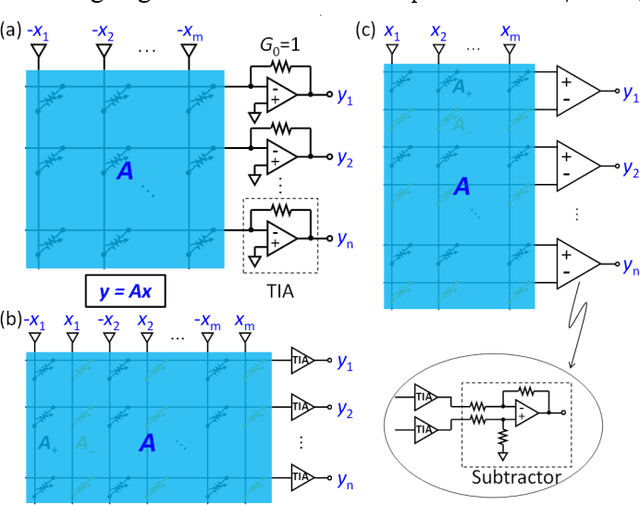
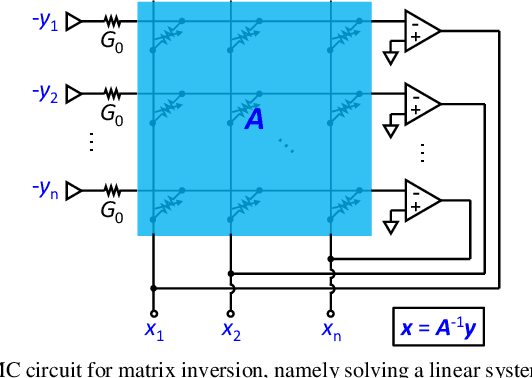
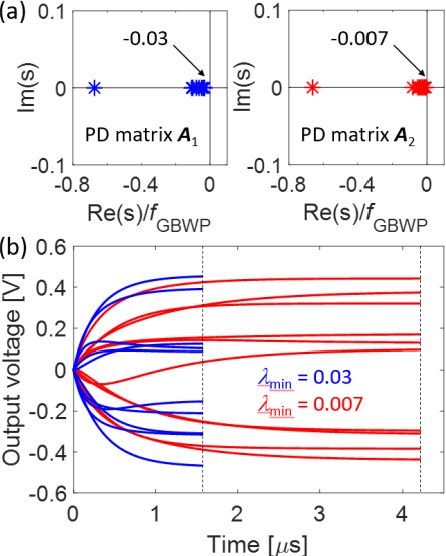
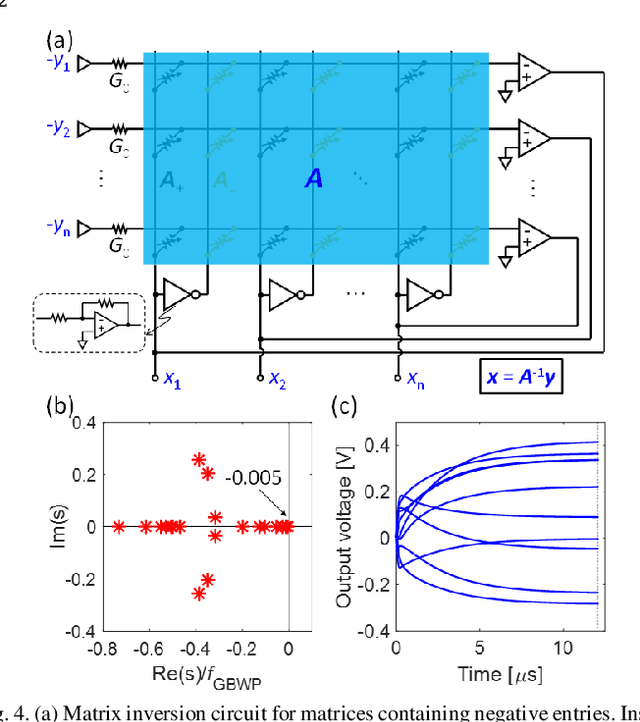
Matrix computation is ubiquitous in modern scientific and engineering fields. Due to the high computational complexity in conventional digital computers, matrix computation represents a heavy workload in many data-intensive applications, e.g., machine learning, scientific computing, and wireless communications. For fast, efficient matrix computations, analog computing with resistive memory arrays has been proven to be a promising solution. In this Tutorial, we present analog matrix computing (AMC) circuits based on crosspoint resistive memory arrays. AMC circuits are able to carry out basic matrix computations, including matrix multiplication, matrix inversion, pseudoinverse and eigenvector computation, all with one single operation. We describe the main design principles of the AMC circuits, such as local/global or negative/positive feedback configurations, with/without external inputs. Mapping strategies for matrices containing negative values will be presented. The underlying requirements for circuit stability will be described via the transfer function analysis, which also defines time complexity of the circuits towards steady-state results. Lastly, typical applications, challenges, and future trends of AMC circuits will be discussed.

One-step regression and classification with crosspoint resistive memory arrays

Machine learning has been getting a large attention in the recent years, as a tool to process big data generated by ubiquitous sensors in our daily life. High speed, low energy computing machines are in demand to enable real-time artificial intelligence at the edge, i.e., without the support of a remote frame server in the cloud. Such requirements challenge the complementary metal-oxide-semiconductor (CMOS) technology, which is limited by the Moore's law approaching its end and the communication bottleneck in conventional computing architecture. Novel computing concepts, architectures and devices are thus strongly needed to accelerate data-intensive applications. Here we show a crosspoint resistive memory circuit with feedback configuration can execute linear regression and logistic regression in just one step by computing the pseudoinverse matrix of the data within the memory. The most elementary learning operation, that is the regression of a sequence of data and the classification of a set of data, can thus be executed in one single computational step by the novel technology. One-step learning is further supported by simulations of the prediction of the cost of a house in Boston and the training of a 2-layer neural network for MNIST digit recognition. The results are all obtained in one computational step, thanks to the physical, parallel, and analog computing within the crosspoint array.