A Tale of Two Approximations: Tightening Over-Approximation for DNN Robustness Verification via Under-Approximation

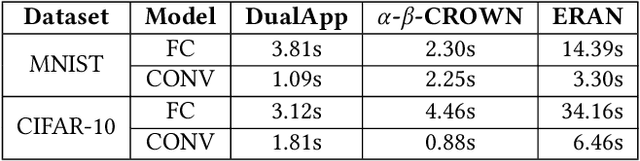
The robustness of deep neural networks (DNNs) is crucial to the hosting system's reliability and security. Formal verification has been demonstrated to be effective in providing provable robustness guarantees. To improve its scalability, over-approximating the non-linear activation functions in DNNs by linear constraints has been widely adopted, which transforms the verification problem into an efficiently solvable linear programming problem. Many efforts have been dedicated to defining the so-called tightest approximations to reduce overestimation imposed by over-approximation. In this paper, we study existing approaches and identify a dominant factor in defining tight approximation, namely the approximation domain of the activation function. We find out that tight approximations defined on approximation domains may not be as tight as the ones on their actual domains, yet existing approaches all rely only on approximation domains. Based on this observation, we propose a novel dual-approximation approach to tighten over-approximations, leveraging an activation function's underestimated domain to define tight approximation bounds. We implement our approach with two complementary algorithms based respectively on Monte Carlo simulation and gradient descent into a tool called DualApp. We assess it on a comprehensive benchmark of DNNs with different architectures. Our experimental results show that DualApp significantly outperforms the state-of-the-art approaches with 100% - 1000% improvement on the verified robustness ratio and 10.64% on average (up to 66.53%) on the certified lower bound.

Boosting Verified Training for Robust Image Classifications via Abstraction

This paper proposes a novel, abstraction-based, certified training method for robust image classifiers. Via abstraction, all perturbed images are mapped into intervals before feeding into neural networks for training. By training on intervals, all the perturbed images that are mapped to the same interval are classified as the same label, rendering the variance of training sets to be small and the loss landscape of the models to be smooth. Consequently, our approach significantly improves the robustness of trained models. For the abstraction, our training method also enables a sound and complete black-box verification approach, which is orthogonal and scalable to arbitrary types of neural networks regardless of their sizes and architectures. We evaluate our method on a wide range of benchmarks in different scales. The experimental results show that our method outperforms state of the art by (i) reducing the verified errors of trained models up to 95.64%; (ii) totally achieving up to 602.50x speedup; and (iii) scaling up to larger models with up to 138 million trainable parameters. The demo is available at https://github.com/zhangzhaodi233/ABSCERT.git.

DualApp: Tight Over-Approximation for Neural Network Robustness Verification via Under-Approximation

The robustness of neural networks is fundamental to the hosting system's reliability and security. Formal verification has been proven to be effective in providing provable robustness guarantees. To improve the verification scalability, over-approximating the non-linear activation functions in neural networks by linear constraints is widely adopted, which transforms the verification problem into an efficiently solvable linear programming problem. As over-approximations inevitably introduce overestimation, many efforts have been dedicated to defining the tightest possible approximations. Recent studies have however showed that the existing so-called tightest approximations are superior to each other. In this paper we identify and report an crucial factor in defining tight approximations, namely the approximation domains of activation functions. We observe that existing approaches only rely on overestimated domains, while the corresponding tight approximation may not necessarily be tight on its actual domain. We propose a novel under-approximation-guided approach, called dual-approximation, to define tight over-approximations and two complementary under-approximation algorithms based on sampling and gradient descent. The overestimated domain guarantees the soundness while the underestimated one guides the tightness. We implement our approach into a tool called DualApp and extensively evaluate it on a comprehensive benchmark of 84 collected and trained neural networks with different architectures. The experimental results show that DualApp outperforms the state-of-the-art approximation-based approaches, with up to 71.22% improvement to the verification result.