Disentangling Shared and Task-Specific Representations from Multi-Modal Clinical Data

Real-world clinical data is inherently multimodal, providing complementary evidence that mirrors the practical necessity of jointly assessing multiple related outcomes. Although multi-task learning can improve efficiency by sharing information across outcomes, existing approaches often fail to balance shared representation learning with outcome-specific modeling. Hard parameter sharing can trigger negative transfer when task gradients conflict, while flexible sharing may still entangle shared and task-specific signals. To address this, we propose a multi-task framework built on a unified Transformer for multimodal fusion, augmented with Orthogonal Task Decomposition (OrthTD) to split patient representations into shared and task-specific subspaces and impose a geometric orthogonality constraint to reduce redundancy and isolate task-specific signals. We evaluated OrthTD on a real-world cohort of 12,430 surgical patients for predicting four outcomes. OrthTD achieved average AUC (area under the receiver operating characteristic curve) of 87.5% and average AUPRC (area under the precision-recall curve) of 37.2%, consistently outperformed advanced tabular and multi-task methods. Notably, OrthTD achieves substantial gains in AUPRC, indicating superior performance in identifying rare events within imbalanced clinical data. These results suggest that enforcing non-redundant shared and task-specific representations can improve multi-outcome prediction from multimodal clinical data.

Matching and mixing: Matchability of graphs under Markovian error

We consider the problem of graph matching for a sequence of graphs generated under a time-dependent Markov chain noise model. Our edgelighter error model, a variant of the classical lamplighter random walk, iteratively corrupts the graph $G_0$ with edge-dependent noise, creating a sequence of noisy graph copies $(G_t)$. Much of the graph matching literature is focused on anonymization thresholds in edge-independent noise settings, and we establish novel anonymization thresholds in this edge-dependent noise setting when matching $G_0$ and $G_t$. Moreover, we also compare this anonymization threshold with the mixing properties of the Markov chain noise model. We show that when $G_0$ is drawn from an Erdős-Rényi model, the graph matching anonymization threshold and the mixing time of the edgelighter walk are both of order $Θ(n^2\log n)$. We further demonstrate that for more structured model for $G_0$ (e.g., the Stochastic Block Model), graph matching anonymization can occur in $O(n^α\log n)$ time for some $α<2$, indicating that anonymization can occur before the Markov chain noise model globally mixes. Through extensive simulations, we verify our theoretical bounds in the settings of Erdős-Rényi random graphs and stochastic block model random graphs, and explore our findings on real-world datasets derived from a Facebook friendship network and a European research institution email communication network.

Dual Attention Driven Lumbar Magnetic Resonance Image Feature Enhancement and Automatic Diagnosis of Herniation

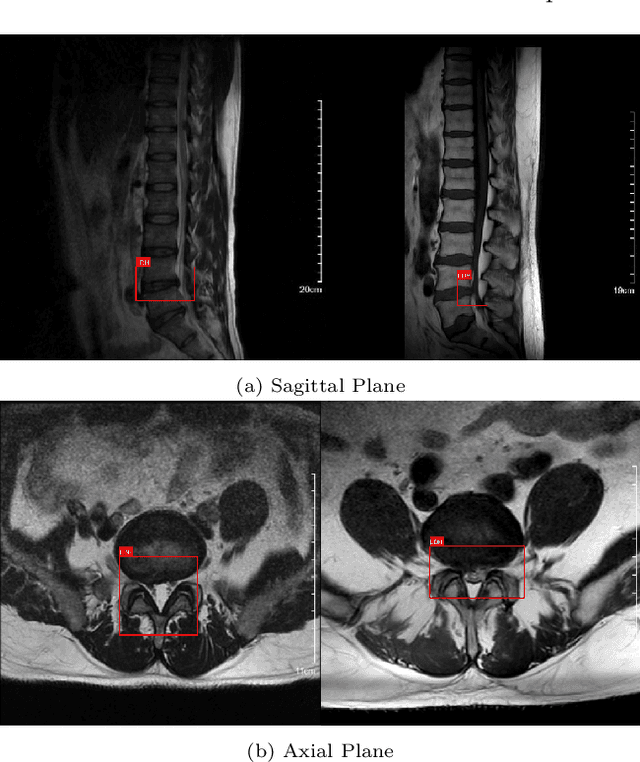
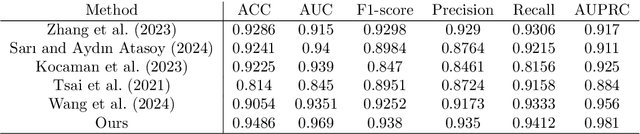
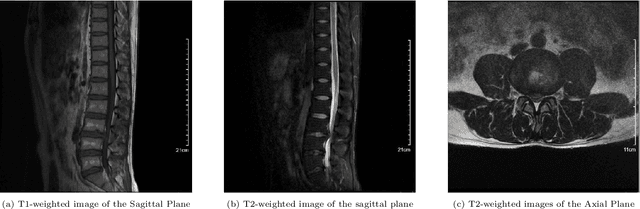
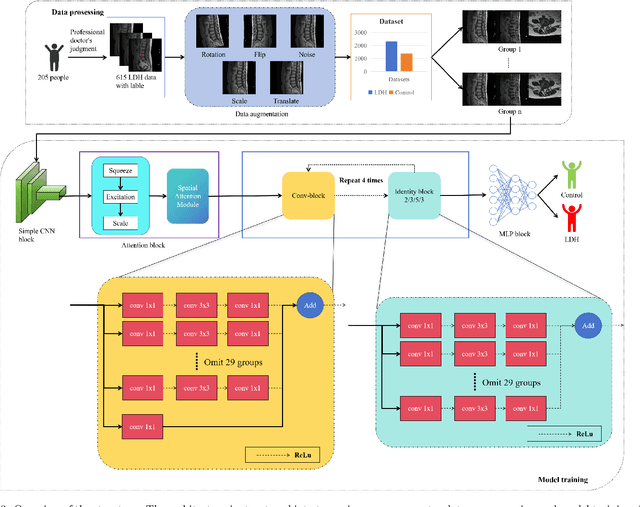
Lumbar disc herniation (LDH) is a common musculoskeletal disease that requires magnetic resonance imaging (MRI) for effective clinical management. However, the interpretation of MRI images heavily relies on the expertise of radiologists, leading to delayed diagnosis and high costs for training physicians. Therefore, this paper proposes an innovative automated LDH classification framework. To address these key issues, the framework utilizes T1-weighted and T2-weighted MRI images from 205 people. The framework extracts clinically actionable LDH features and generates standardized diagnostic outputs by leveraging data augmentation and channel and spatial attention mechanisms. These outputs can help physicians make confident and time-effective care decisions when needed. The proposed framework achieves an area under the receiver operating characteristic curve (AUC-ROC) of 0.969 and an accuracy of 0.9486 for LDH detection. The experimental results demonstrate the performance of the proposed framework. Our framework only requires a small number of datasets for training to demonstrate high diagnostic accuracy. This is expected to be a solution to enhance the LDH detection capabilities of primary hospitals.

Gotta match 'em all: Solution diversification in graph matching matched filters

We present a novel approach for finding multiple noisily embedded template graphs in a very large background graph. Our method builds upon the graph-matching-matched-filter technique proposed in Sussman et al., with the discovery of multiple diverse matchings being achieved by iteratively penalizing a suitable node-pair similarity matrix in the matched filter algorithm. In addition, we propose algorithmic speed-ups that greatly enhance the scalability of our matched-filter approach. We present theoretical justification of our methodology in the setting of correlated Erdos-Renyi graphs, showing its ability to sequentially discover multiple templates under mild model conditions. We additionally demonstrate our method's utility via extensive experiments both using simulated models and real-world dataset, include human brain connectomes and a large transactional knowledge base.

Clustered Graph Matching for Label Recovery and Graph Classification

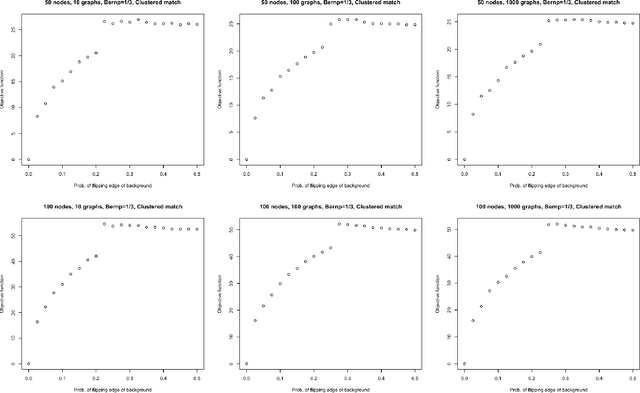
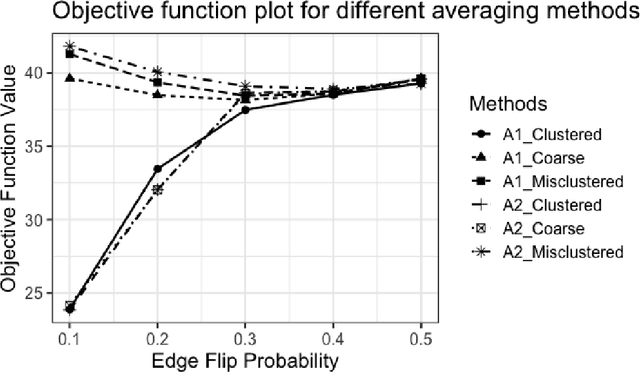
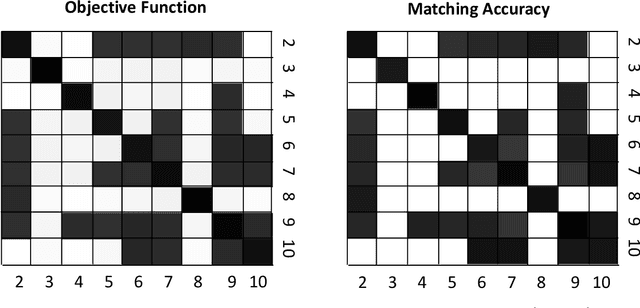
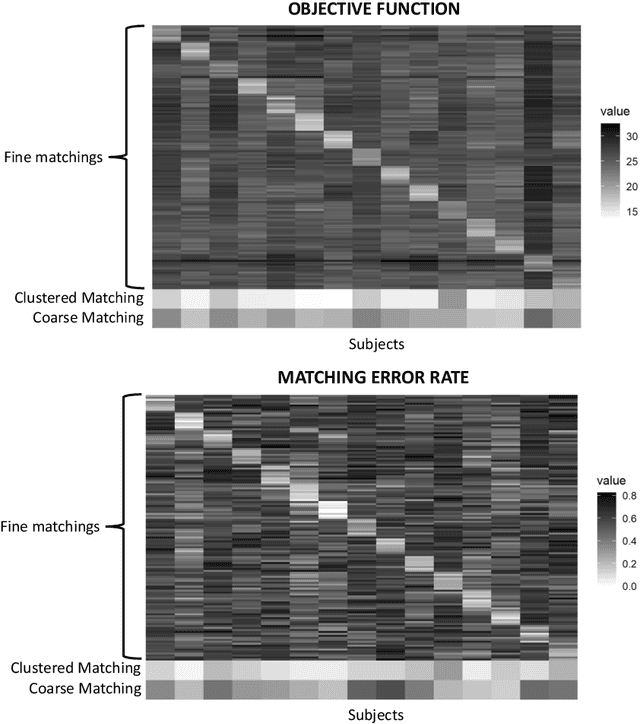
Given a collection of vertex-aligned networks and an additional label-shuffled network, we propose procedures for leveraging the signal in the vertex-aligned collection to recover the labels of the shuffled network. We consider matching the shuffled network to averages of the networks in the vertex-aligned collection at different levels of granularity. We demonstrate both in theory and practice that if the graphs come from different network classes, then clustering the networks into classes followed by matching the new graph to cluster-averages can yield higher fidelity matching performance than matching to the global average graph. Moreover, by minimizing the graph matching objective function with respect to each cluster average, this approach simultaneously classifies and recovers the vertex labels for the shuffled graph.