Clustered Graph Matching for Label Recovery and Graph Classification
Paper and Code
May 06, 2022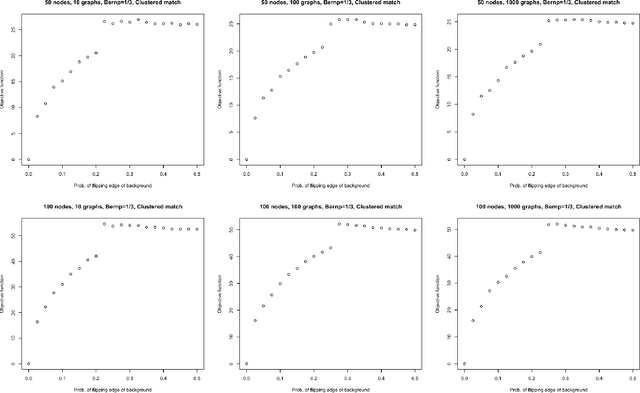
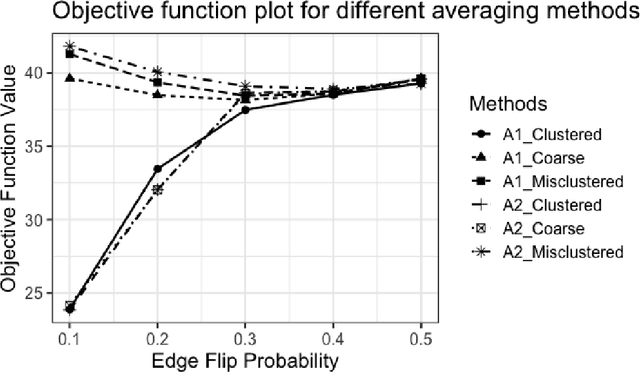
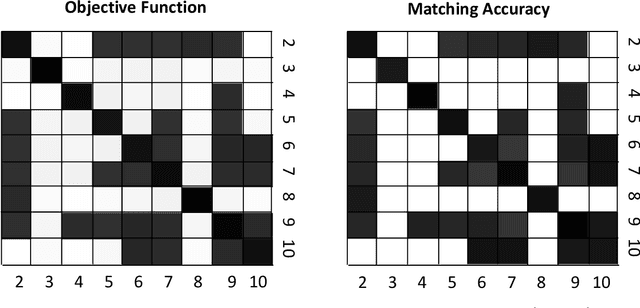
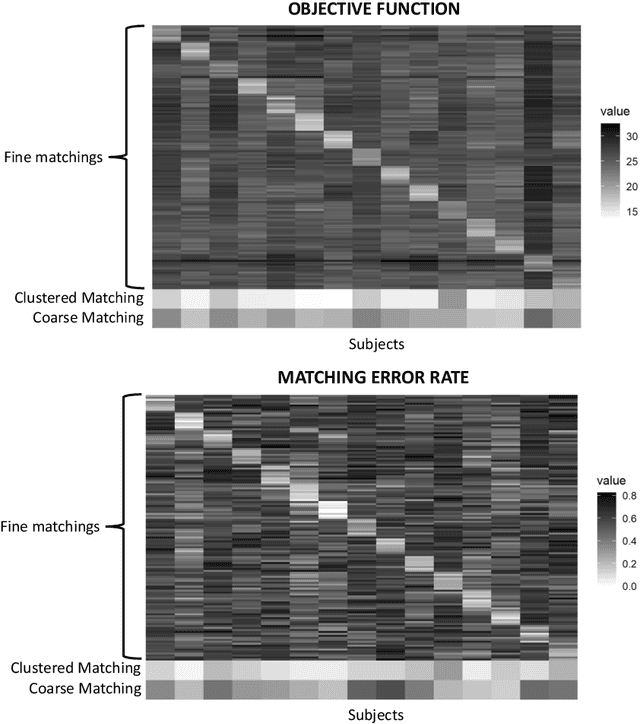
Given a collection of vertex-aligned networks and an additional label-shuffled network, we propose procedures for leveraging the signal in the vertex-aligned collection to recover the labels of the shuffled network. We consider matching the shuffled network to averages of the networks in the vertex-aligned collection at different levels of granularity. We demonstrate both in theory and practice that if the graphs come from different network classes, then clustering the networks into classes followed by matching the new graph to cluster-averages can yield higher fidelity matching performance than matching to the global average graph. Moreover, by minimizing the graph matching objective function with respect to each cluster average, this approach simultaneously classifies and recovers the vertex labels for the shuffled graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge