Toward Robust Neural Networks via Sparsification

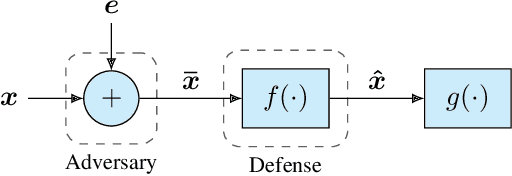
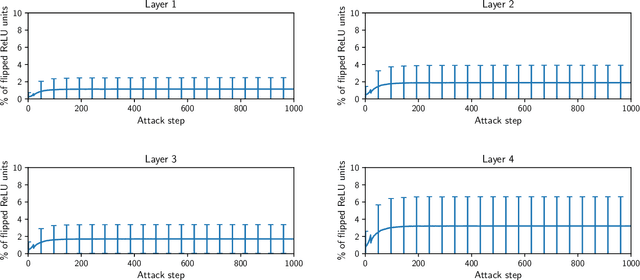
It is by now well-known that small adversarial perturbations can induce classification errors in deep neural networks. In this paper, we make the case that a systematic exploitation of sparsity is key to defending against such attacks, and that a "locally linear" model for neural networks can be used to develop a theoretical foundation for crafting attacks and defenses. We consider two defenses. The first is a sparsifying front end, which attenuates the impact of the attack by a factor of roughly $K/N$ where $N$ is the data dimension and $K$ is the sparsity level. The second is sparsification of network weights, which attenuates the worst-case growth of an attack as it flows up the network. We also devise attacks based on the locally linear model that outperform the well-known FGSM attack. We provide experimental results for the MNIST and Fashion-MNIST datasets, showing the efficacy of the proposed sparsity-based defenses.

Combating Adversarial Attacks Using Sparse Representations

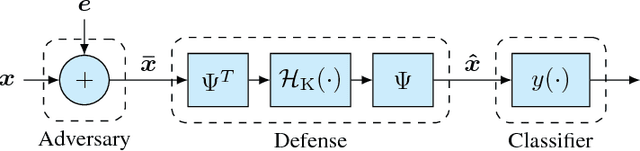
It is by now well-known that small adversarial perturbations can induce classification errors in deep neural networks (DNNs). In this paper, we make the case that sparse representations of the input data are a crucial tool for combating such attacks. For linear classifiers, we show that a sparsifying front end is provably effective against $\ell_{\infty}$-bounded attacks, reducing output distortion due to the attack by a factor of roughly $K / N$ where $N$ is the data dimension and $K$ is the sparsity level. We then extend this concept to DNNs, showing that a "locally linear" model can be used to develop a theoretical foundation for crafting attacks and defenses. Experimental results for the MNIST dataset show the efficacy of the proposed sparsifying front end.

Sparsity-based Defense against Adversarial Attacks on Linear Classifiers

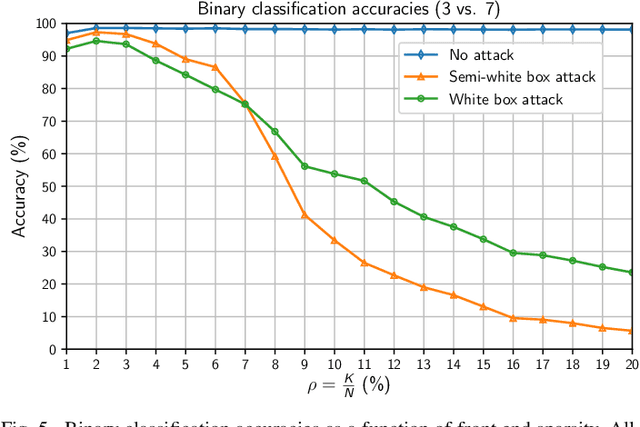
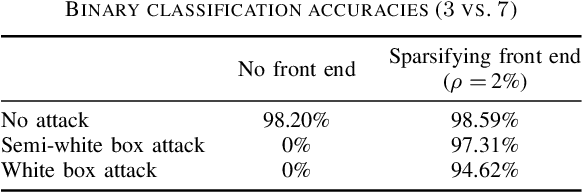
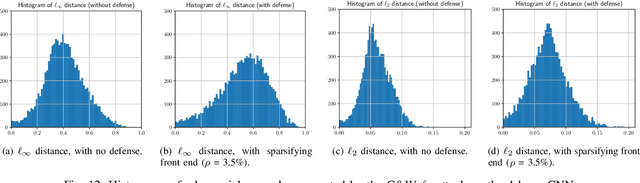
Deep neural networks represent the state of the art in machine learning in a growing number of fields, including vision, speech and natural language processing. However, recent work raises important questions about the robustness of such architectures, by showing that it is possible to induce classification errors through tiny, almost imperceptible, perturbations. Vulnerability to such "adversarial attacks", or "adversarial examples", has been conjectured to be due to the excessive linearity of deep networks. In this paper, we study this phenomenon in the setting of a linear classifier, and show that it is possible to exploit sparsity in natural data to combat $\ell_{\infty}$-bounded adversarial perturbations. Specifically, we demonstrate the efficacy of a sparsifying front end via an ensemble averaged analysis, and experimental results for the MNIST handwritten digit database. To the best of our knowledge, this is the first work to show that sparsity provides a theoretically rigorous framework for defense against adversarial attacks.

On the information in spike timing: neural codes derived from polychronous groups

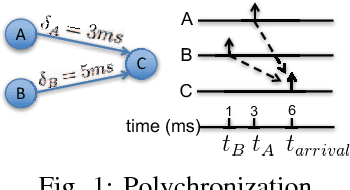
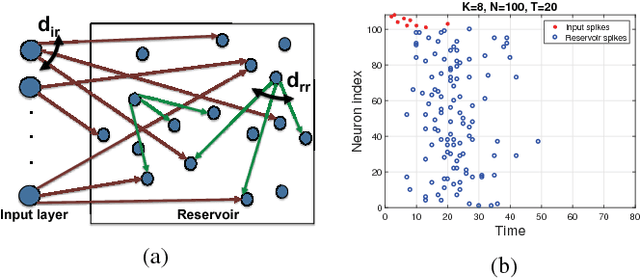
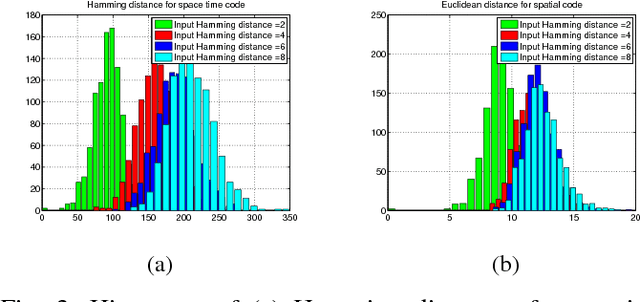
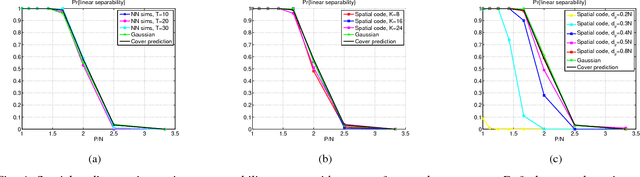
There is growing evidence regarding the importance of spike timing in neural information processing, with even a small number of spikes carrying information, but computational models lag significantly behind those for rate coding. Experimental evidence on neuronal behavior is consistent with the dynamical and state dependent behavior provided by recurrent connections. This motivates the minimalistic abstraction investigated in this paper, aimed at providing insight into information encoding in spike timing via recurrent connections. We employ information-theoretic techniques for a simple reservoir model which encodes input spatiotemporal patterns into a sparse neural code, translating the polychronous groups introduced by Izhikevich into codewords on which we can perform standard vector operations. We show that the distance properties of the code are similar to those for (optimal) random codes. In particular, the code meets benchmarks associated with both linear classification and capacity, with the latter scaling exponentially with reservoir size.